ГДЗ по Математике 5 Класс Часть 2 Номер 204 Мнемозина Виленкин, Жохов — Подробные Ответы

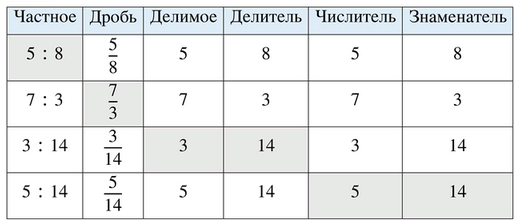
Заполните пустые клетки таблицы:

В данном задании рассматривается деление чисел, представленное в виде частного, и его запись в виде дроби. Частное — это результат деления одного числа на другое. В таблице показано, как каждое частное соответствует дроби, где числитель — это делимое, а знаменатель — делитель. Например, в первом случае частное \(5 : 8\) записывается как дробь \(\frac{5}{8}\), где 5 — числитель, а 8 — знаменатель. Это отражает основное свойство дроби: числитель показывает, сколько частей взято, а знаменатель — на сколько частей разделено целое.

Делимое и делитель — ключевые элементы при преобразовании деления в дробь. Делимое — это число, которое делят, а делитель — число, на которое делят. При записи дроби делимое становится числителем, а делитель — знаменателем. Например, для частного \(7 : 3\), делимое 7 становится числителем дроби \(\frac{7}{3}\), а делитель 3 — знаменателем. Такая запись помогает визуально и математически представить частное в виде дроби, что удобно для дальнейших вычислений и анализа.

В таблице также показаны другие примеры с разными значениями делимого и делителя, например, \(3 : 14\) и \(5 : 14\). В каждом случае дробь формируется аналогично: числитель равен делимому, а знаменатель — делителю. Это универсальное правило, которое позволяет легко переходить от операции деления к дробной записи. Такой подход упрощает понимание дробей и их связь с делением, а также облегчает выполнение арифметических действий с дробями.