ГДЗ по Математике 5 Класс Часть 2 Номер 201 Мнемозина Виленкин, Жохов — Подробные Ответы

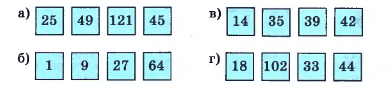
Четвёртый лишний. В каждом ряду три числа обладают общим свойством, а одно число этим свойством не обладает. Укажите, что это за свойство и какое число лишнее.

а) Число 45 является лишним, так как остальные числа — квадраты натуральных чисел:
\( 25 = 5^2 \), \( 49 = 7^2 \), \( 121 = 11^2 \).

б) Число 9 является лишним, так как остальные числа — кубы натуральных чисел:
\( 1 = 1^3 \), \( 27 = 3^3 \), \( 64 = 4^3 \).

в) Число 39 является лишним, так как оно единственное из данных чисел, не кратное 7:
\( 14 = 2 \cdot 7 \), \( 35 = 5 \cdot 7 \), \( 42 = 6 \cdot 7 \).

г) Число 33 является лишним, так как оно нечётное, а остальные — чётные.
Число 44 является лишним, так как оно единственное из данных чисел, не кратное 3:
\( 18 = 3 \cdot 6 \), \( 102 = 3 \cdot 34 \), \( 33 = 3 \cdot 11 \).

а) Число 45 является лишним, потому что остальные числа в наборе — это квадраты натуральных чисел. Квадрат натурального числа — это число, полученное возведением этого числа в степень 2. Например, \( 25 = 5^2 \), \( 49 = 7^2 \), \( 121 = 11^2 \). Все эти числа получены возведением натуральных чисел 5, 7 и 11 в квадрат. Число 45 не является квадратом никакого натурального числа, так как нет такого \( n \in \mathbb{N} \), что \( n^2 = 45 \). Поэтому оно выделяется из ряда.

Если рассмотреть числа по их свойствам, то квадраты имеют строго определённые значения, и любое число, не удовлетворяющее этому условию, будет выбиваться из общей закономерности. В данном случае 45 — не квадрат, а просто натуральное число, поэтому оно и считается лишним в этом наборе.

б) Число 9 является лишним, так как остальные числа — это кубы натуральных чисел. Куб натурального числа — это число, полученное возведением натурального числа в степень 3. В данном наборе: \( 1 = 1^3 \), \( 27 = 3^3 \), \( 64 = 4^3 \). Все эти числа являются кубами, а число 9 не может быть представлено в виде \( n^3 \) для натурального \( n \), ведь \( 2^3 = 8 \), а \( 3^3 = 27 \), и 9 не попадает в эту последовательность. Поэтому 9 выделяется как исключение.

Кубы обладают определённой структурой и закономерностью, которая выражается в частоте появления чисел и их значениях. Число 9 не удовлетворяет этому условию, поэтому оно не вписывается в ряд и считается лишним.

в) Число 39 является лишним, так как оно единственное из данных чисел, не кратное 7. Кратность числу 7 означает, что число можно представить в виде произведения 7 на другое натуральное число. В данном случае: \( 14 = 2 \cdot 7 \), \( 35 = 5 \cdot 7 \), \( 42 = 6 \cdot 7 \). Все эти числа делятся на 7 без остатка. Число 39 же не делится на 7, так как \( \frac{39}{7} \) не является целым числом. Это делает 39 исключением из ряда.

Кратность — важное свойство, которое помогает классифицировать числа по определённым признакам. Если одно число не удовлетворяет этому условию, оно выделяется из общего множества.

г) Число 33 является лишним, так как оно нечётное, а остальные числа — чётные. Чётные числа делятся на 2 без остатка, а нечётные — нет. В данном наборе все числа, кроме 33, делятся на 2, а 33 не делится, так как \( \frac{33}{2} \) не является целым числом. Это делает 33 исключением.

Число 44 является лишним, потому что оно единственное из данных чисел, не кратное 3. Кратность 3 означает, что число можно представить как произведение 3 на другое число. В данном наборе: \( 18 = 3 \cdot 6 \), \( 102 = 3 \cdot 34 \), \( 33 = 3 \cdot 11 \). Все эти числа делятся на 3 без остатка. Число 44 не делится на 3, так как \( \frac{44}{3} \) не является целым числом, что выделяет его из ряда.