ГДЗ по Математике 5 Класс Часть 2 Номер 178 Мнемозина Виленкин, Жохов — Подробные Ответы

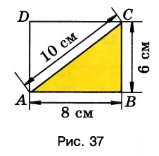
Вычислите периметр и площадь треугольника \(ABC\) (рис. 37).

\(P_{\triangle ABC} = 10 + 6 + 8 = 24 \, (\text{см})\).

Площадь \(\triangle ABC\) равна половине площади четырёхугольника \(ABCD\).

\(S_{\triangle ABC} = \frac{8 \cdot 6}{2} = \frac{48}{2} = 24 \, (\text{см}^2)\).

Ответ: \(P_{\triangle ABC} = 24 \, \text{см}\); \(S_{\triangle ABC} = 24 \, \text{см}^2\).

\(P_{\triangle ABC} = 10 + 6 + 8 = 24 \, (\text{см})\).

Периметр треугольника \(ABC\) вычисляется как сумма длин всех его сторон. В данном случае стороны равны 10 см, 6 см и 8 см. Складывая эти значения, получаем \(24\) см, что и есть полный периметр треугольника. Это важно, поскольку периметр показывает общий размер фигуры по её границе.

Площадь треугольника \(ABC\) равна половине площади четырёхугольника \(ABCD\). Для нахождения площади треугольника используется формула площади прямоугольного треугольника или треугольника с известными основаниями и высотой. Здесь даны длины основания и высоты: \(8\) см и \(6\) см соответственно. Формула площади треугольника — это произведение основания на высоту, делённое на два, то есть \(S_{\triangle ABC} = \frac{8 \cdot 6}{2}\).

Вычисляя, получаем \(48\) делённое на \(2\), что равно \(24 \, \text{см}^2\). Это значит, что площадь треугольника \(ABC\) составляет ровно половину площади четырехугольника \(ABCD\), если площадь всего четырехугольника равна \(48 \, \text{см}^2\). Таким образом, мы имеем точные значения и для периметра, и для площади треугольника.

Ответ: \(P_{\triangle ABC} = 24 \, \text{см}\); \(S_{\triangle ABC} = 24 \, \text{см}^2\).