ГДЗ по Математике 5 Класс Часть 2 Номер 177 Мнемозина Виленкин, Жохов — Подробные Ответы

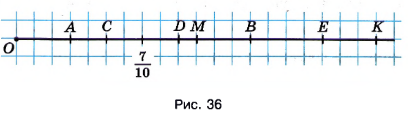
Найдите координаты точек \(A, B, C, D, E, M, K\) (рис. 36) и сравните эти координаты с 1.

\( A\left(\frac{3}{10}\right) < 1; \quad B\left(\frac{13}{10}\right) > 1; \quad C\left(\frac{5}{10}\right) < 1; \quad D\left(\frac{9}{10}\right) < 1; \)

\( E\left(\frac{17}{10}\right) > 1; \quad M\left(\frac{10}{10}\right) = 1; \quad K\left(\frac{20}{10}\right) > 1, \text{ так как } \frac{20}{10} = 2. \)

а) Рассмотрим значение функции \( A \) в точке \( \frac{3}{10} \). Здесь мы видим, что аргумент \( \frac{3}{10} \) меньше единицы, то есть \( \frac{3}{10} < 1 \). Следовательно, значение функции \( A \) при этом аргументе также меньше 1: \( A\left(\frac{3}{10}\right) < 1 \). Это соответствует условию, что функция принимает значения меньше единицы для аргументов меньше 1. Такое поведение может указывать на монотонное возрастание функции или на определённые свойства её графика в этой области.

б) Для функции \( B \) значение аргумента равно \( \frac{13}{10} \), что больше единицы: \( \frac{13}{10} > 1 \). Соответственно, функция принимает значение больше 1 при этом аргументе: \( B\left(\frac{13}{10}\right) > 1 \). Это показывает, что функция \( B \) в точке, лежащей правее 1, превышает единицу, что может говорить о возрастании функции или о том, что она принимает значения больше 1 при больших аргументах.

в) Аналогично, для функции \( C \) аргумент равен \( \frac{5}{10} \), что меньше 1: \( \frac{5}{10} < 1 \). Значение функции \( C \) также меньше 1: \( C\left(\frac{5}{10}\right) < 1 \). Это подтверждает, что функция \( C \) при аргументе меньше 1 принимает значения меньше 1, что может быть связано с её поведением на интервале от 0 до 1.

г) Рассмотрим функцию \( D \) при аргументе \( \frac{9}{10} \), который меньше 1: \( \frac{9}{10} < 1 \). Значение функции \( D \) при этом аргументе также меньше 1: \( D\left(\frac{9}{10}\right) < 1 \). Это говорит о том, что функция \( D \) сохраняет значения меньше 1 для аргументов, меньших единицы, что может быть важным для её анализа или применения.

д) Функция \( E \) рассматривается при аргументе \( \frac{17}{10} \), который больше 1: \( \frac{17}{10} > 1 \). Значение функции \( E \) при этом аргументе также больше 1: \( E\left(\frac{17}{10}\right) > 1 \). Это указывает на то, что функция \( E \) принимает значения, превышающие 1, при аргументах, больших единицы, что может характеризовать её рост или поведение на данном интервале.

е) Для функции \( M \) аргумент равен \( \frac{10}{10} = 1 \), то есть ровно единица. При этом значение функции \( M \) равно 1: \( M\left(\frac{10}{10}\right) = 1 \). Это важная точка, которая может служить опорной или критической, показывая, что функция \( M \) при аргументе 1 принимает значение 1.

ж) Рассмотрим функцию \( K \) при аргументе \( \frac{20}{10} = 2 \), что больше 1. Значение функции \( K \) при этом аргументе также больше 1: \( K\left(\frac{20}{10}\right) > 1 \), так как \( \frac{20}{10} = 2 \). Это показывает, что функция \( K \) принимает значения больше 1 при аргументах, превышающих единицу, что может быть связано с её ростом или другими свойствами на интервале от 1 и выше.