ГДЗ по Математике 5 Класс Часть 2 Номер 146 Мнемозина Виленкин, Жохов — Подробные Ответы

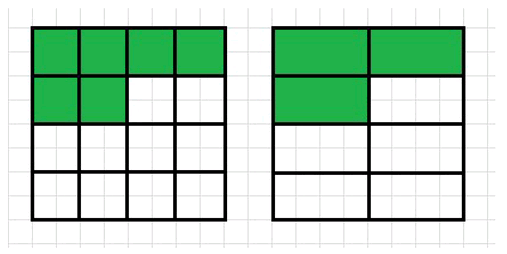
Начертите квадрат со стороной 4 см. Покажите на чертеже: \(\frac{6}{16}\) квадрата, \(\frac{3}{8}\) квадрата. Найдите площади этих частей квадрата и объясните полученный результат.

\(S_{\text{квадрата}} = 4^2 = 16 \, \text{см}^2.\)

Площадь \(\frac{6}{16}\) квадрата:
\(16 : 16 \cdot 6 = 6 \, \text{см}^2.\)

Площадь \(\frac{3}{8}\) квадрата:
\(16 : 8 \cdot 3 = 2 \cdot 3 = 6 \, \text{см}^2.\)

Следовательно, \(\frac{6}{16} = \frac{3}{8}.\)

\(S_{\text{квадрата}} = 4^2 = 16 \, \text{см}^2\). Это полная площадь исходного квадрата со стороной 4 см. Сначала мы вычисляем площадь всего квадрата, так как она необходима для определения долей, которые занимают выделенные части. Площадь квадрата равна квадрату длины его стороны, поэтому \(4^2 = 16\).

Площадь, соответствующая части, выделенной на первой сетке, равна \(\frac{6}{16}\) площади квадрата. Это можно понять, если сосчитать количество зеленых маленьких клеток — их 6 из 16 всего. Для нахождения площади этой части нужно умножить общую площадь квадрата на эту дробь: \(16 \cdot \frac{6}{16} = 6 \, \text{см}^2\). Деление и умножение здесь взаимно компенсируют друг друга, поэтому результат равен 6.

Площадь, выделенная на второй сетке, соответствует дроби \(\frac{3}{8}\) от площади квадрата. Для проверки равенства долей нужно вычислить, сколько будет составлять эта часть: \(16 \cdot \frac{3}{8} = 16 : 8 \cdot 3 = 2 \cdot 3 = 6 \, \text{см}^2\). Таким образом, площадь выделенной части во втором случае тоже равна 6 см², что доказывает равенство дробей \(\frac{6}{16} = \frac{3}{8}\).