ГДЗ по Математике 5 Класс Часть 2 Номер 141 Мнемозина Виленкин, Жохов — Подробные Ответы

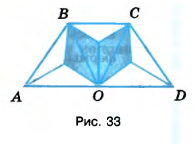
Какая часть четырёхугольника \(ABCD\) (рис. 33) закрашена? Какая часть осталась незакрашенной?

Закрашена часть четырёхугольника \(ABCD\), которая составляет \(\frac{4}{9}\) от всей площади этого четырёхугольника. Это означает, что если площадь всего четырёхугольника принять за единицу, то закрашенная область занимает именно \(\frac{4}{9}\) этой площади. Такой способ выражения части фигуры через дробь позволяет точно определить, какая доля от целого объекта была выделена или изменена. В данном случае, дробь \(\frac{4}{9}\) указывает, что из девяти равных частей всего четырёхугольника закрашено четыре.

Остальная часть четырёхугольника, которая не закрашена, составляет разницу между целым четырёхугольником и закрашенной частью. Поскольку вся площадь равна 1, а закрашено \(\frac{4}{9}\), то оставшаяся незакрашенная часть будет равна \(1 — \frac{4}{9}\). Выполним вычитание: \(1 = \frac{9}{9}\), следовательно, незакрашенная часть равна \(\frac{9}{9} — \frac{4}{9} = \frac{5}{9}\). Это значит, что оставшаяся незакрашенная область занимает \(\frac{5}{9}\) от площади всего четырёхугольника \(ABCD\).

Таким образом, мы видим, что площадь четырёхугольника делится на две части: закрашенную и незакрашенную, которые вместе дают полную площадь фигуры. Закрашенная часть — это \(\frac{4}{9}\), а незакрашенная — \(\frac{5}{9}\), и сумма этих частей равна единице, то есть площади всего четырёхугольника. Такой подход позволяет легко понять, как распределяется площадь внутри фигуры и как части взаимосвязаны через простые дроби.