ГДЗ по Математике 5 Класс Часть 2 Номер 135 Мнемозина Виленкин, Жохов — Подробные Ответы

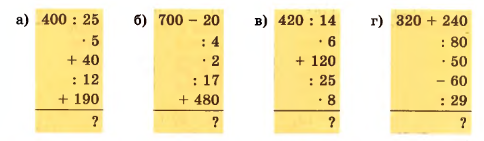
Вычислите устно:

а) Сначала делим число 400 на 25, потому что в условии указано действие деления: \(400 : 25 = 16\). Это означает, что 400 разделили на 25 частей, и каждая часть равна 16. Далее умножаем полученное число 16 на 5, чтобы увеличить значение в 5 раз: \(16 \cdot 5 = 80\). Это действие показывает, как меняется число при умножении.

После этого к 80 прибавляем 40, что означает сложение двух чисел: \(80 + 40 = 120\). Следующий шаг — деление 120 на 12, то есть распределение 120 на 12 равных частей: \(120 : 12 = 10\). Наконец, к результату прибавляем 190, что даёт итоговое значение: \(10 + 190 = 200\). Последовательность операций показывает, как с помощью деления, умножения и сложения можно получить нужный результат.

б) Начинаем с вычитания 20 из 700, чтобы уменьшить число: \(700 — 20 = 680\). Это действие уменьшает исходное число на заданное количество. Затем делим полученное число 680 на 4, что даёт 170: \(680 : 4 = 170\). Деление показывает, на сколько частей можно разделить число.

После этого умножаем 170 на 2, увеличивая значение в 2 раза: \(170 \cdot 2 = 340\). Следующий шаг — деление 340 на 17, что даёт 20: \(340 : 17 = 20\). Заканчиваем сложением 20 и 480, чтобы получить итог: \(20 + 480 = 500\). Такой порядок действий позволяет последовательно преобразовать число, используя различные арифметические операции.

в) Сначала делим 420 на 14, чтобы узнать, сколько раз 14 помещается в 420: \(420 : 14 = 30\). Это базовое деление, которое часто используется для разбиения на равные части. Затем умножаем 30 на 6, увеличивая число в 6 раз: \(30 \cdot 6 = 180\). Следующее действие — сложение 180 и 120, что даёт сумму 300: \(180 + 120 = 300\).

Далее делим 300 на 25, чтобы найти, сколько раз 25 помещается в 300: \(300 : 25 = 12\). Завершаем умножением 12 на 8, что даёт 96: \(12 \cdot 8 = 96\). Эта последовательность операций показывает, как с помощью деления, умножения и сложения можно преобразовать исходные числа и получить конечный результат.

г) Начинаем с сложения 320 и 240, чтобы получить сумму: \(320 + 240 = 560\). Это простое арифметическое действие, объединяющее два числа. Затем делим 560 на 80, чтобы узнать, сколько раз 80 помещается в 560: \(560 : 80 = 7\). Это деление показывает, как можно разделить число на равные части.

После этого умножаем 7 на 50, увеличивая число в 50 раз: \(7 \cdot 50 = 350\). Следующий шаг — вычитание 60 из 350, что даёт 290: \(350 — 60 = 290\). Заканчиваем делением 290 на 29, чтобы получить итоговое число: \(290 : 29 = 10\). Такая последовательность действий помогает последовательно изменять значения, используя основные арифметические операции.