ГДЗ по Математике 5 Класс Часть 2 Номер 126 Мнемозина Виленкин, Жохов — Подробные Ответы

Отметьте на луче точки с координатами:

\(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \frac{5}{4}, \frac{6}{4}, \frac{7}{4}, \frac{8}{4}\)

За единичный отрезок примите длину 12 клеток тетради.

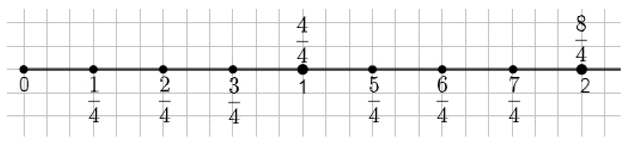
На числовой прямой отмечены точки:
\(0, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, 1, \frac{5}{4}, \frac{6}{4}, \frac{7}{4}, 2\).

Расстояние между соседними точками равно \(\frac{1}{4}\).
Точки расположены в порядке возрастания с шагом \(\frac{1}{4}\), начиная с 0 и заканчивая 2.

На числовой прямой изображены точки, расположенные в определённом порядке. Начинается последовательность с числа 0, которое является начальной точкой отсчёта. Далее идут дробные значения, выраженные в виде дробей с числителем от 1 до 7 и знаменателем 4, то есть \(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{5}{4}, \frac{6}{4}, \frac{7}{4}\). После них следует целое число 1, которое находится между \(\frac{3}{4}\) и \(\frac{5}{4}\), а в конце отметка 2. Таким образом, все точки расположены на числовой прямой по возрастанию, с равными промежутками.

Расстояние между соседними точками равно \(\frac{1}{4}\). Это видно из того, что если взять любую пару соседних точек, например \(0\) и \(\frac{1}{4}\), или \(\frac{5}{4}\) и \(\frac{6}{4}\), то разница между ними равна \(\frac{1}{4}\). Это означает, что шаг между точками постоянен и равен четверти единицы. Таким образом, числовая прямая разбита на равные отрезки длиной \(\frac{1}{4}\), что позволяет удобно измерять и сравнивать значения.

В целом, данное расположение точек показывает, как можно представить дробные и целые числа на числовой прямой, используя равномерное деление отрезка между 0 и 2 на части длиной \(\frac{1}{4}\). Это наглядно демонстрирует принцип дробления целого числа на равные части и расположения дробей в порядке возрастания, что является основой для понимания дробных чисел и их местоположения на числовой оси.