ГДЗ по Математике 5 Класс Часть 2 Номер 116 Мнемозина Виленкин, Жохов — Подробные Ответы

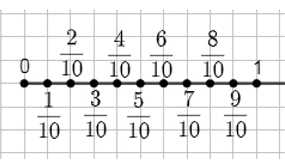
Примите за единичный отрезок длину 10 клеток тетради и отметьте на координатном луче числа:

\(\frac{1}{10}; \frac{2}{10}; \frac{3}{10}; \frac{4}{10}; \frac{5}{10}; \frac{6}{10}; \frac{7}{10}; \frac{8}{10}; \frac{9}{10}\).

На координатной оси длиной 10 клеток отмечены точки, соответствующие числам: \(\frac{1}{10}; \frac{2}{10}; \frac{3}{10}; \frac{4}{10}; \frac{5}{10}; \frac{6}{10}; \frac{7}{10}; \frac{8}{10}; \frac{9}{10}\).

Ответ: эти числа расположены на координатной оси в точках, соответствующих дробям, где числитель — номер деления, а знаменатель — 10.

a) На координатной оси длиной 10 клеток отмечены точки, соответствующие дробям, где числитель — номер деления, а знаменатель — 10. Каждая точка на оси показывает конкретное значение, равное доле от всей длины. Так как длина отрезка равна 10 клеткам, то каждое деление делит этот отрезок на равные части, и каждая часть соответствует одной десятой части.

Значения, которые нужно отметить, — это дроби вида \(\frac{n}{10}\), где \(n\) — целое число от 1 до 9. Каждое число показывает, сколько десятых составляет данное значение. Например, \(\frac{1}{10}\) — это одна десятая часть от всей длины, а \(\frac{9}{10}\) — девять десятых. Эти числа расположены на оси в точках, которые соответствуют делениям, начиная с первой деления после начала (0) и заканчивая перед концом (10).

Поскольку деления равномерные, то каждое число занимает свою позицию, равную длине, пропорциональной числителю дроби. В итоге, точки, соответствующие дробям \(\frac{1}{10}\), \(\frac{2}{10}\), \(\frac{3}{10}\), …, \(\frac{9}{10}\), расположены строго между началом и концом отрезка, на равных интервалах. Эти точки показывают конкретные доли общей длины отрезка, что позволяет легко визуализировать, как дроби со знаменателем 10 разбивают отрезок на равные части.

b) Важно понять, что дроби вида \(\frac{n}{10}\) — это именно десятичные доли, которые делят весь отрезок на 10 равных частей. Каждая часть имеет длину, равную одной десятой от всей длины, то есть 1 клетке, если считать по условию. Таким образом, каждое число, которое нужно отметить, — это точка на оси, которая находится на расстоянии, равном \(n\) делений, где каждое деление равно 1 клетке. Это означает, что дроби \(\frac{1}{10}\), \(\frac{2}{10}\), и так далее, по сути, показывают, сколько целых делений пройдено от начала оси, если считать по одной клетке за одно деление.

На практике, эти дроби соответствуют точкам, расположенным в точках, которые можно определить как произведение числителя на длину одного деления. Поскольку длина всего отрезка — 10 клеток, то длина одного деления равна 1 клетке. Следовательно, дробь \(\frac{n}{10}\) занимает позицию, равную \(n\) клеткам от начала. Это позволяет легко понять, что дроби \(\frac{1}{10}\) до \(\frac{9}{10}\) — это просто точки, расположенные на оси в интервале между 0 и 1, разделённом на 10 равных частей.

Таким образом, отмечая эти числа на оси, мы визуализируем дроби, являющиеся десятичными долями, и получаем наглядное представление о том, как дроби со знаменателем 10 распределяются по отрезку длиной 10 клеток. Каждая точка показывает конкретное значение, соответствующее определенной доле от всей длины, что помогает понять пропорциональность и равномерность делений.