ГДЗ по Математике 5 Класс Часть 2 Номер 1071 Мнемозина Виленкин, Жохов — Подробные Ответы

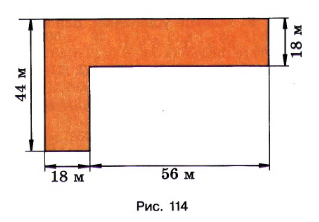
Вычислите в арах площадь участка, изображённого на рисунке 114.

Разделим участок на два прямоугольника. Первый с сторонами \(44 \text{ м}\) и \(18 \text{ м}\), второй с сторонами \(56 \text{ м}\) и \(18 \text{ м}\).

Найдём площадь каждого прямоугольника и сложим:

\(44 \cdot 18 + 56 \cdot 18 = 18 \cdot (44 + 56) = 18 \cdot 100 = 1800 \text{ м}^2\).

Переведём площадь в сотки:

\(1800 \text{ м}^2 = 18 \text{ а}\).

Ответ: 18 а.

Разделим участок на два прямоугольника, чтобы упростить вычисление площади. Первый прямоугольник имеет стороны 44 м и 18 м. Это означает, что длина одного прямоугольника равна 44 метрам, а ширина — 18 метрам. Второй прямоугольник имеет стороны 56 м и 18 м, то есть его длина 56 метров, а ширина совпадает с первым — 18 метров. Такое разбиение удобно, так как обе фигуры имеют одинаковую ширину, что позволит использовать общие множители при вычислении площади.

Для нахождения площади каждого прямоугольника используем формулу площади прямоугольника: произведение длины на ширину. Площадь первого прямоугольника равна \(44 \cdot 18\), а площадь второго — \(56 \cdot 18\). Чтобы найти общую площадь участка, нужно сложить площади двух прямоугольников. Так как ширина у обоих прямоугольников одинаковая, можно вынести 18 за скобки и записать сумму площадей как \(18 \cdot (44 + 56)\).

Выполним сложение внутри скобок: \(44 + 56 = 100\). Теперь площадь всего участка равна \(18 \cdot 100 = 1800\) квадратных метров. Для удобства измерения площади земельных участков её часто переводят в сотки, где 1 сотка равна 100 квадратным метрам. Тогда \(1800 \text{ м}^2\) равны \( \frac{1800}{100} = 18\) соткам. Таким образом, площадь всего участка составляет 18 соток.