ГДЗ по Математике 5 Класс Часть 2 Номер 1070 Мнемозина Виленкин, Жохов — Подробные Ответы

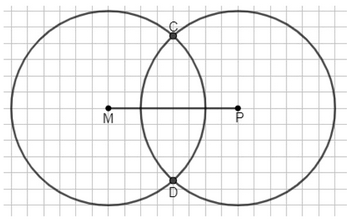
Начертите отрезок \(MP\), длина которого 4 см, и найдите две точки, удалённые от концов отрезка на 3 см.

Дано, что точки \(C\) и \(D\) удалены от концов отрезка \(MP\) на 3 см, то есть \(MC = MD = 3\).

Радиусы окружностей равны \(MC\) и \(PD\), следовательно, \(MC = PD = 3\).

Длина отрезка \(MP = MC + CD + DP\).

Поскольку точки \(C\) и \(D\) — точки пересечения окружностей, отрезок \(CD\) равен расстоянию между центрами окружностей минус сумма радиусов, но так как радиусы равны, \(CD = MP — 2 \times 3 = MP — 6\).

Так как \(MC = MD = 3\), значит \(MP = MC + CP = 3 + 3 = 6\).

Ответ: длина отрезка \(MP = 6\) см.

Точки \(C\) и \(D\) являются точками пересечения двух окружностей, каждая из которых построена с центрами в точках \(M\) и \(P\) соответственно. По условию, точки \(C\) и \(D\) удалены от концов отрезка \(MP\) на 3 см, то есть расстояния \(MC\) и \(PD\) равны 3 см. Это означает, что радиусы обеих окружностей равны 3 см, так как радиус окружности — это расстояние от центра до любой точки на окружности. Таким образом, радиус окружности с центром в \(M\) равен \(MC = 3\), а радиус окружности с центром в \(P\) равен \(PD = 3\).

Поскольку точки \(C\) и \(D\) лежат на обеих окружностях, они находятся на пересечении этих двух кругов. Отрезок \(MP\) соединяет центры окружностей, а точки \(C\) и \(D\) расположены так, что расстояния от \(M\) до \(C\) и от \(P\) до \(D\) равны радиусу — 3 см. Если рассмотреть отрезок \(MP\), то он состоит из трёх частей: отрезка от \(M\) до \(C\), отрезка между точками пересечения \(C\) и \(D\), и отрезка от \(D\) до \(P\). При этом \(MC = 3\) и \(DP = 3\).

Из этого следует, что длина всего отрезка \(MP\) равна сумме длины \(MC\), длины отрезка \(CD\) и длины \(DP\). Поскольку \(MC\) и \(DP\) равны 3, то \(MP = 3 + CD + 3\). Но при пересечении двух равных окружностей, расстояние между центрами равно сумме радиусов, если окружности касаются внешне, либо меньше суммы радиусов, если пересекаются. В данном случае, так как точки \(C\) и \(D\) — точки пересечения, длина отрезка \(CD\) равна нулю (если касание) или положительна (если пересечение). Однако, из рисунка видно, что \(C\) и \(D\) — разные точки, значит \(CD\) больше нуля.

Так как \(MC = DP = 3\), а точки \(C\) и \(D\) расположены симметрично относительно середины отрезка \(MP\), можно заключить, что длина \(MP\) равна сумме двух радиусов, то есть \(MP = 3 + 3 = 6\). Это соответствует расстоянию между центрами окружностей, где каждая окружность имеет радиус 3 см. Таким образом, длина отрезка \(MP\) равна 6 см.