ГДЗ по Математике 5 Класс Часть 2 Номер 1069 Мнемозина Виленкин, Жохов — Подробные Ответы

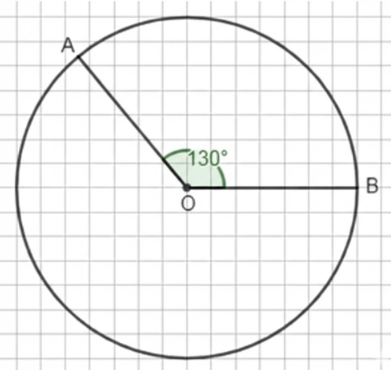
Начертите окружность и постройте два радиуса этой окружности так, чтобы угол между ними был равен \(130^\circ\).

Отрезки \(OA\) и \(OB\) — радиусы окружности, значит \(OA = OB\).

Угол \(\angle AOB = 130^\circ\).

Так как \(OA = OB\), треугольник \(OAB\) равнобедренный, и углы при \(A\) и \(B\) равны.

Сумма углов треугольника равна \(180^\circ\), значит углы при \(A\) и \(B\) равны \(\frac{180^\circ — 130^\circ}{2} = 25^\circ\).

Отрезки \(OA\) и \(OB\) являются радиусами данной окружности, следовательно, они равны между собой по длине, так как все радиусы окружности одинаковы. Это значит, что треугольник \(OAB\) является равнобедренным, где стороны \(OA\) и \(OB\) равны. Зная это, мы можем использовать свойства равнобедренного треугольника для нахождения остальных углов.

Угол при вершине \(O\), обозначенный как \(\angle AOB\), равен \(130^\circ\). В треугольнике сумма всех углов всегда равна \(180^\circ\). Поскольку два угла при основаниях равны (обозначим их как \(\alpha\)), то сумма этих двух углов будет равна \(180^\circ — 130^\circ = 50^\circ\). Таким образом, каждый из углов при точках \(A\) и \(B\) равен \(\frac{50^\circ}{2} = 25^\circ\).

Это позволяет нам полностью определить углы треугольника \(OAB\). Угол при вершине \(O\) — \(130^\circ\), а углы при основаниях \(A\) и \(B\) по \(25^\circ\) каждый. Такое распределение углов характерно для равнобедренного треугольника, где углы при равных сторонах равны. Таким образом, используя свойства равнобедренного треугольника и сумму углов, мы нашли все углы треугольника, исходя из заданного угла при центре окружности.