ГДЗ по Математике 5 Класс Часть 2 Номер 1066 Мнемозина Виленкин, Жохов — Подробные Ответы

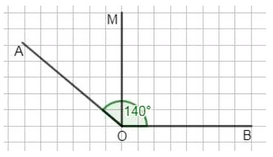
Постройте угол \(AOB\) в \(140^\circ\) и проведите луч \(OM\) так, чтобы он разделил угол \(AOB\) на два угла, один из которых на \(40^\circ\) больше другого.

Пусть \(\angle AOM = x^\circ\), тогда \(\angle MOB = (x + 40)^\circ\).

Составим уравнение:
\(x + (x + 40) = 140\)
\(2x = 140 — 40\)
\(2x = 100\)
\(x = 50^\circ = \angle AOM\).

Тогда
\(x + 40 = 50 + 40 = 90^\circ = \angle MOB\).

Пусть \(\angle AOM = x^\circ\). Это обозначение означает, что мы рассматриваем угол между лучами \(AO\) и \(OM\) и обозначаем его величину через переменную \(x\). Далее в условии сказано, что угол \(\angle MOB\) на \(40^\circ\) больше угла \(\angle AOM\), то есть \(\angle MOB = (x + 40)^\circ\). Это важно, потому что сумма этих двух углов равна \(140^\circ\), что можно записать уравнением \(x + (x + 40) = 140\). Здесь мы используем свойство, что сумма углов \(AOM\) и \(MOB\) равна \(140^\circ\), что видно из рисунка.

Решая уравнение, сначала раскрываем скобки: \(x + x + 40 = 140\), что упрощается до \(2x + 40 = 140\). Чтобы найти \(x\), нужно избавиться от числа \(40\) с левой части, для этого вычтем \(40\) из обеих частей уравнения, получим \(2x = 140 — 40\). После вычисления разности справа, получаем \(2x = 100\). Теперь, чтобы найти \(x\), делим обе части уравнения на \(2\), получаем \(x = \frac{100}{2} = 50^\circ\).

Таким образом, угол \(\angle AOM\) равен \(50^\circ\). Теперь подставим это значение в выражение для угла \(\angle MOB\), которое равно \(x + 40\). Подставляя \(x = 50^\circ\), получаем \(\angle MOB = 50 + 40 = 90^\circ\). Это совпадает с тем, что угол \(\angle MOB\) равен \(90^\circ\), как показано на рисунке. Таким образом, мы нашли величины углов, исходя из их суммы и разницы, используя простое линейное уравнение.