ГДЗ по Математике 5 Класс Часть 2 Номер 1065 Мнемозина Виленкин, Жохов — Подробные Ответы

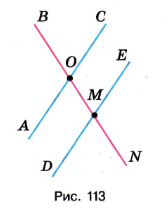
Измерьте углы \(AOB\), \(BOC\), \(DMN\), \(NME\) (рис. 113). Какие из этих углов равны?Измерьте углы \(AOB\), \(BOC\), \(DMN\), \(NME\) (рис. 113). Какие из этих углов равны?

Угол \( \angle AOB = \angle NME = 115^\circ \).

Угол \( \angle BOC = \angle DMN = 65^\circ \).

Угол \( \angle AOB \) равен углу \( \angle NME \), и оба они составляют \( 115^\circ \). Это означает, что два угла, обозначенные как \( \angle AOB \) и \( \angle NME \), имеют одинаковую величину, равную 115 градусов. Такое равенство углов может возникать, например, если данные углы являются соответственными или равными по условию задачи, либо если они образованы при пересечении параллельных прямых с секущей.

Для угла \( \angle BOC \) и угла \( \angle DMN \) указано, что они равны и составляют \( 65^\circ \). Это значит, что эти два угла также имеют одинаковую меру, равную 65 градусов. Обычно равенство таких углов указывает на симметрию или равенство между соответствующими частями геометрической фигуры, что может быть использовано для доказательства равенств или вычислений других углов.

Таким образом, исходя из данных значений, можно утверждать, что в рассматриваемой геометрической конфигурации углы \( \angle AOB \) и \( \angle NME \) равны \( 115^\circ \), а углы \( \angle BOC \) и \( \angle DMN \) равны \( 65^\circ \). Это равенство углов часто служит основой для дальнейших построений и вычислений в задачах, связанных с углами и их свойствами.