ГДЗ по Математике 5 Класс Часть 2 Номер 104 Мнемозина Виленкин, Жохов — Подробные Ответы

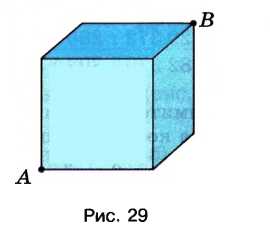
Попробуйте найти самый короткий путь по поверхности куба от точки \(A\) к точке \(B\) (рис. 29). Сколько таких путей можно указать?

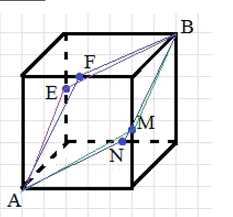
От точки \( A \) к точке \( B \) можно попасть кратчайшими путями:

\( ANB; AMB; AEB; AFB \).

Существует четыре таких маршрута.

Ответ: четыре.

От точки \( A \) к точке \( B \) можно попасть разными путями, но нас интересуют только кратчайшие маршруты. В данном кубе точки \( A \) и \( B \) находятся на противоположных вершинах, а значит кратчайший путь — это путь, который проходит по ребрам куба, минимально увеличивая длину пути. Для этого нужно рассмотреть все возможные варианты, где можно дойти от \( A \) до \( B \), проходя через промежуточные точки, расположенные на ребрах куба, при этом не отклоняясь от кратчайшего расстояния. Кратчайший путь в кубе между противоположными вершинами состоит из трёх ребер, так как длина ребра равна 1, и для перехода от одной вершины к противоположной нужно пройти ровно три ребра.

В нашем случае кратчайшие пути проходят через точки \( N \), \( M \), \( E \) и \( F \), которые расположены на ребрах куба и соединяют вершины \( A \) и \( B \). Рассмотрим каждый маршрут по отдельности: \( ANB \) — путь от \( A \) через \( N \) к \( B \), \( AMB \) — через \( M \), \( AEB \) — через \( E \), и \( AFB \) — через \( F \). Все эти маршруты состоят из трёх звеньев, что соответствует минимальному числу ребер, необходимых для перехода между \( A \) и \( B \). Таким образом, все они являются кратчайшими.

Поскольку все четыре маршрута различны и каждый из них минимален по длине, то общее число кратчайших путей от точки \( A \) к точке \( B \) равно четырём. Это подтверждается тем, что в кубе существует ровно четыре способа пройти от одной вершины к противоположной, изменяя координаты по одному измерению за раз в любом порядке, и каждая из точек \( N, M, E, F \) соответствует одному из этих вариантов. Следовательно, ответ: четыре.