ГДЗ по Математике 5 Класс Часть 2 Номер 1037 Мнемозина Виленкин, Жохов — Подробные Ответы

Запишите все трёхзначные числа, для записи которых используются только цифры 3 и 0.

Дано: цифры 3 и 0.

Трехзначное число состоит из трех разрядов: сотни, десятки и единицы.

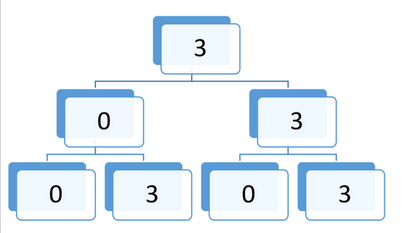
— Первая цифра (сотни) не может быть 0, иначе число будет не трехзначным.
— Значит, первая цифра — 3.
— Вторая и третья цифры могут быть либо 0, либо 3.

Возможные варианты:

300; 303; 330; 333.

Ответ: 300; 303; 330; 333.

Трехзначные числа состоят из трех цифр: сотен, десятков и единиц. Для того чтобы число было действительно трехзначным, его первая цифра не может быть равна нулю, так как тогда число станет двухзначным или меньше. В нашем случае цифры для составления чисел ограничены только двумя вариантами — 3 и 0. Значит, первая цифра обязательно должна быть 3, чтобы число оставалось трехзначным.

Вторая и третья цифры могут принимать любое значение из множества {0, 3}. Это связано с тем, что в позициях десятков и единиц число может содержать либо ноль, либо три, без ограничений. Таким образом, для каждой из этих двух позиций есть два варианта выбора цифры: либо 0, либо 3. Это значит, что общее количество вариантов для второй и третьей цифр равно \(2 \times 2 = 2^2 = 4\).

Перечислим все возможные варианты: если вторая цифра 0, а третья 0, то число — 300; если вторая 0, а третья 3 — 303; если вторая 3, а третья 0 — 330; если вторая 3, а третья 3 — 333. Таким образом, все возможные трехзначные числа из цифр 3 и 0: 300, 303, 330, 333. Их ровно четыре, что совпадает с подсчетом вариантов для двух последних цифр.