ГДЗ по Математике 5 Класс Часть 2 Номер 1035 Мнемозина Виленкин, Жохов — Подробные Ответы

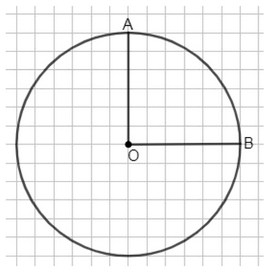
Начертите окружность и проведите два её радиуса, образующие прямой угол.

Угол \( \angle AOB = 90^\circ \) означает, что радиусы \( OA \) и \( OB \) перпендикулярны друг другу.

Так как \( OA \) и \( OB \) — радиусы окружности, то \( OA = OB \).

Точка \( O \) — центр окружности, следовательно, дуга \( AB \) — четверть окружности.

Длина дуги \( AB = \frac{1}{4} \) длины всей окружности.

Длина окружности равна \( 2 \pi r \), где \( r = OA \).

Значит, длина дуги \( AB = \frac{1}{4} \cdot 2 \pi r = \frac{\pi r}{2} \).

Угол \( \angle AOB = 90^\circ \) показывает, что лучи \( OA \) и \( OB \), исходящие из центра окружности \( O \), образуют прямой угол. Поскольку \( O \) — центр окружности, отрезки \( OA \) и \( OB \) являются радиусами этой окружности. Радиусы окружности равны между собой, то есть \( OA = OB = r \), где \( r \) — радиус окружности. Это важно, потому что угол между двумя равными радиусами определяет часть окружности, которую они ограничивают.

Дуга \( AB \), заключённая между точками \( A \) и \( B \) на окружности, соответствует центральному углу \( \angle AOB \). Центральный угол измеряет величину дуги в градусах, поэтому дуга \( AB \) составляет \( 90^\circ \) из полного круга, который равен \( 360^\circ \). Следовательно, длина дуги \( AB \) составляет четверть длины всей окружности, так как \( \frac{90^\circ}{360^\circ} = \frac{1}{4} \). Это означает, что если длина всей окружности равна \( C \), то длина дуги \( AB \) равна \( \frac{1}{4} C \).

Длина окружности вычисляется по формуле \( C = 2 \pi r \), где \( r \) — радиус окружности. Подставляя это значение в формулу для длины дуги, получаем \( AB = \frac{1}{4} \cdot 2 \pi r = \frac{\pi r}{2} \). Таким образом, длина дуги \( AB \) равна половине произведения числа \( \pi \) и радиуса \( r \), что соответствует четверти полной окружности, ограниченной прямым углом в центре.