
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 1034 Мнемозина Виленкин, Жохов — Подробные Ответы
Каким свойством обладают точки окружности? Какой отрезок называют радиусом окружности? Диаметром окружности? Начертите окружность и проведите три радиуса этой окружности и её диаметр.
Все точки окружности равноудалены от ее центра.
Радиус окружности — отрезок, соединяющий любую ее точку с центром.
Диаметр окружности — отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
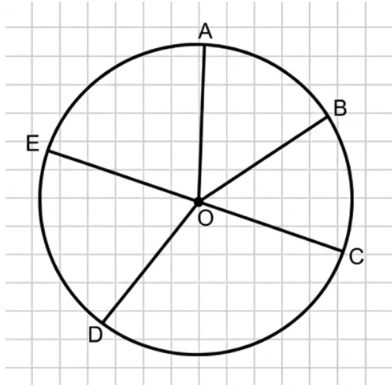
Отрезки \(OA\), \(OB\) и \(OD\) являются радиусами окружности.
Отрезок \(CE\) является диаметром окружности.
Все точки окружности равноудалены от ее центра, что означает, что расстояние от любой точки на окружности до центра одинаково. Это свойство является основным определением окружности и позволяет говорить о равенстве всех радиусов, исходящих из центра к точкам на окружности. Центр окружности — это фиксированная точка, от которой измеряется расстояние до всех точек на окружности. Таким образом, если обозначить центр как точку \(O\), а любую точку на окружности как \(A\), то длина отрезка \(OA\) будет постоянной для всех таких точек.
Радиус окружности — это отрезок, соединяющий центр окружности с любой точкой на ее границе. В нашем случае отрезки \(OA\), \(OB\) и \(OD\) являются радиусами, потому что они соединяют центр \(O\) с точками \(A\), \(B\) и \(D\) на окружности. Длина каждого радиуса одинаковая и обозначается как \(r\). Если взять произвольную точку \(X\) на окружности, то отрезок \(OX\) также будет равен \(r\). Радиус является основным параметром, по которому можно вычислить длину окружности и площадь круга.
Диаметр окружности — это отрезок, который соединяет две точки на окружности и при этом проходит через центр. Диаметр в два раза длиннее радиуса, то есть его длина равна \(2r\). В данном случае отрезок \(CE\) является диаметром, так как он соединяет точки \(C\) и \(E\), лежащие на окружности, и проходит через центр \(O\). Диаметр делит окружность на две равные части и является самой длинной хордой окружности. Если обозначить длину диаметра как \(d\), то будет верно равенство \(d = 2r\), где \(r\) — радиус окружности.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!