
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 2 Номер 1032 Мнемозина Виленкин, Жохов — Подробные Ответы
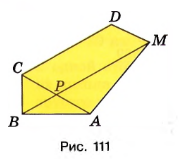
Пятиугольное поле \( ABCDM \), план которого изображён на рисунке 111, разбито на четыре части отрезками \( AC \) и \( BM \). Назовите эти части и найдите площадь поля, если площади треугольных частей равны 50 тыс. м\(^2\), 60 тыс. м\(^2\), 170 тыс. м\(^2\), а четырёхугольной — 380 тыс. м\(^2\).
Поле разбито на части: \( BPC; ABP; APM; CDMP \).
Площадь поля \( ABCDM \) равна:
\( 50 + 60 + 170 + 380 = 110 + 170 + 380 = 280 + 380 = 660 \) тыс. м\(^2\).
Ответ: 660 тыс. м\(^2\).
Поле разбито на четыре части: \( BPC \), \( ABP \), \( APM \), \( CDMP \). Для того чтобы найти общую площадь поля \( ABCDM \), необходимо сложить площади всех этих частей. Каждая часть представляет собой определённую фигуру с известной площадью, и сумма этих площадей даст искомое значение. Это стандартный приём в геометрии, когда сложная фигура разбивается на более простые части, площади которых легче вычислить.
Площадь первой части \( BPC \) равна 50 тыс. м\(^2\), второй части \( ABP \) — 60 тыс. м\(^2\), третьей части \( APM \) — 170 тыс. м\(^2\), а четвёртой части \( CDMP \) — 380 тыс. м\(^2\). Сначала складываем площади первых двух частей: \( 50 + 60 = 110 \) тыс. м\(^2\). Затем к этой сумме добавляем площадь третьей части: \( 110 + 170 = 280 \) тыс. м\(^2\). Наконец, прибавляем площадь четвёртой части: \( 280 + 380 = 660 \) тыс. м\(^2\). Таким образом, мы получили общую площадь всего поля.
Этот способ решения основан на принципе аддитивности площади: площадь объединения непересекающихся частей равна сумме площадей этих частей. Важно, что части поля не перекрываются, и поэтому их площади можно просто сложить. Итоговый результат показывает, что площадь поля \( ABCDM \) составляет 660 тыс. м\(^2\). Это и есть ответ задачи.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!