ГДЗ по Математике 5 Класс Часть 2 Номер 1031 Мнемозина Виленкин, Жохов — Подробные Ответы

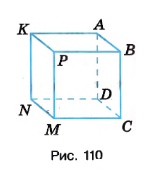
На рисунке 110 изображён куб. Назовите рёбра верхней и нижней граней, переднюю грань, вершины правой грани, равные рёбра.

Ребра верхней грани: \( AB; BP; KP; AK \).

Ребра нижней грани: \( MN; MC; CD; ND \).

Передняя грань: \( MPBC \).

Вершины правой грани: \( A, B, C, D \).

Равные ребра (у куба все ребра равны):
\( MN = CD = AB = KP = NK = MP = BC = AD = MC = ND =\) \(= AK = BP \).

Ребра верхней грани — это отрезки, соединяющие вершины верхней плоскости куба. В данном случае они обозначены как \( AB \), \( BP \), \( KP \), \( AK \). Каждое из этих ребер является частью верхней грани и соединяет соответствующие вершины, образуя квадрат или прямоугольник, в зависимости от формы и ориентации фигуры. Эти ребра важны для понимания структуры верхней поверхности, так как они ограничивают её и задают форму.

Ребра нижней грани представлены отрезками \( MN \), \( MC \), \( CD \), \( ND \). Аналогично верхней грани, эти ребра соединяют вершины нижней плоскости. Они образуют замкнутый контур, определяющий нижнюю грань куба или параллелепипеда. Важно отметить, что нижняя грань параллельна верхней, и ребра обеих граней обычно равны по длине, что характерно для куба.

Передняя грань обозначена как \( MPBC \). Это множество вершин, соединённых ребрами, которые формируют переднюю плоскость фигуры. Здесь \( M \), \( P \), \( B \), \( C \) — вершины, расположенные так, что при соединении они образуют плоскую поверхность, видимую спереди. Эта грань помогает понять ориентацию фигуры в пространстве и служит ориентиром для определения остальных граней.

Вершины правой грани перечислены как \( A, B, C, D \). Эти точки задают правую боковую плоскость фигуры. Соединение этих вершин ребрами формирует грань, которая находится справа относительно наблюдателя. Понимание расположения вершин правой грани необходимо для полного представления о трёхмерной структуре и взаимном расположении граней.

Все ребра куба равны по длине, что является основным свойством куба. В данном случае равенство ребер выражается формулой: \( MN = CD = AB = KP = NK = MP = BC = AD = MC = ND = AK = BP \). Это означает, что длины всех перечисленных ребер совпадают, что подтверждает, что фигура является кубом или правильным параллелепипедом с равными рёбрами. Такое равенство гарантирует, что все грани являются квадратами, а фигура обладает симметрией и равномерностью.