ГДЗ по Математике 5 Класс Часть 2 Номер 103 Мнемозина Виленкин, Жохов — Подробные Ответы

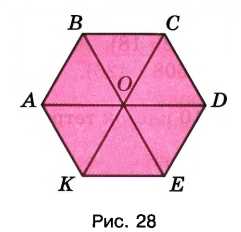
Какую часть на рисунке 28 составляет:

а) треугольник \(ABO\) от четырёхугольника \(ABCO\);

б) треугольник \(ABO\) от четырёхугольника \(ABCD\);

в) четырёхугольник \(ABCO\) от четырёхугольника \(ABCD\);

г) четырёхугольник \(ABCO\) от шестиугольника \(ABCDEK\)?

а) Площадь треугольника \( ABO \) составляет \(\frac{1}{2}\) часть от площади четырёхугольника \( ABCO \).

б) Площадь треугольника \( ABO \) составляет \(\frac{1}{3}\) часть от площади четырёхугольника \( ABCO \).

в) Площадь четырёхугольника \( ABCO \) составляет \(\frac{2}{3}\) часть от площади четырёхугольника \( ABCD \).

г) Площадь четырёхугольника \( ABCO \) составляет \(\frac{2}{6}\) часть от площади шестиугольника \( ABCDEK \).

а) Треугольник \( ABO \) занимает ровно половину площади четырёхугольника \( ABCO \). Это означает, что если площадь четырёхугольника равна \( S \), то площадь треугольника \( ABO \) будет равна \( \frac{1}{2}S \). Такое соотношение возникает, когда треугольник образован диагональю четырёхугольника, которая делит его на две равные части.

Для определения доли площади треугольника в четырёхугольнике важно понимать, что диагональ \( AO \) разбивает фигуру на два треугольника, и если они равны по площади, то каждый из них занимает половину от площади всего четырёхугольника. Поэтому утверждение, что треугольник \( ABO \) составляет \( \frac{1}{2} \) часть четырёхугольника \( ABCO \), верно.

б) В данном случае площадь треугольника \( ABO \) равна одной трети площади четырёхугольника \( ABCO \). Это возможно, если четырёхугольник разбит на три части, одна из которых — треугольник \( ABO \). Например, если внутри четырёхугольника проведены дополнительные линии, которые делят его на три равные по площади части, тогда площадь треугольника будет составлять \( \frac{1}{3} \) от площади всего четырёхугольника.

Такое соотношение показывает, что треугольник \( ABO \) меньше, чем в предыдущем случае, и занимает меньшую часть площади четырёхугольника. Это может быть связано с расположением точек и формой четырёхугольника, которые влияют на пропорции площадей.

в) Четырёхугольник \( ABCO \) занимает \( \frac{2}{3} \) часть площади более крупного четырёхугольника \( ABCD \). Это значит, что площадь \( ABCO \) равна двум третям площади \( ABCD \). Такое соотношение указывает на то, что \( ABCO \) является частью \( ABCD \), но не всей его площадью, а именно большей её частью.

Это может происходить, если \( ABCO \) — это фигура, образованная внутри \( ABCD \), например, срез или часть, ограниченная некоторыми линиями, которые уменьшают площадь исходного четырёхугольника до двух третей. Таким образом, площадь \( ABCO \) меньше площади \( ABCD \), но всё же занимает значительную её часть.

г) Четырёхугольник \( ABCO \) занимает \(\frac{2}{6}\) часть площади шестиугольника \( ABCDEK \). Это означает, что \( ABCO \) — это часть шестиугольника, которая равна одной третьей его площади, поскольку \(\frac{2}{6} = \frac{1}{3}\).

Такое соотношение говорит о том, что шестиугольник \( ABCDEK \) можно разбить на несколько частей, и четырёхугольник \( ABCO \) занимает одну из этих частей, примерно треть от всей площади шестиугольника. Это возможно, если \( ABCO \) является частью шестиугольника, ограниченной определёнными его сторонами или диагоналями, которые делят фигуру на равные или пропорциональные области.