ГДЗ по Математике 5 Класс Часть 2 Номер 1001 Мнемозина Виленкин, Жохов — Подробные Ответы

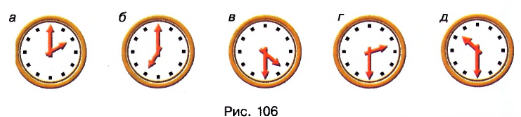
Не пользуясь транспортиром, определите угол между стрелками часов на рисунке 106.

Так как половина циферблата — это \(180^\circ\), то 5 мин — это \( \frac{180}{6} = 30^\circ \).

a) \(30 \cdot 2 = 60^\circ\);

б) \(30 \cdot 5 = 150^\circ\);

в) \(30 + \frac{30}{2} = 30 + 15 = 45^\circ\);

г) \(30 \cdot 3 + \frac{30}{2} = 90 + 15 = 105^\circ\);

д) \(30 \cdot 4 + \frac{30}{2} = 120 + 15 = 135^\circ\).

а) Половина циферблата равна \(180^\circ\), что соответствует 30 минутам. Значит, каждые 5 минут соответствуют углу, который равен \( \frac{180}{6} = 30^\circ \), так как 30 минут делятся на 6 частей по 5 минут. Чтобы найти угол за 2 таких интервала по 5 минут, умножаем 30 на 2, получаем \(30 \cdot 2 = 60^\circ\). Это означает, что за 10 минут стрелка часов проходит угол в 60 градусов.

Далее, это значение важно, так как оно показывает, как быстро движется стрелка за определённое время. Угол измеряется в градусах, а время — в минутах, поэтому умножение на количество интервалов даёт искомый угол.

б) Аналогично, если 5 минут соответствуют углу в \(30^\circ\), то за 5 таких интервалов по 5 минут угол будет равен \(30 \cdot 5 = 150^\circ\). Это значит, что за 25 минут стрелка часов пройдет угол в 150 градусов. Здесь мы просто умножаем угол за один интервал на количество интервалов, чтобы получить общий угол.

Этот метод позволяет легко находить угол, пройденный стрелкой за любое количество минут, если известен угол за 5 минут.

в) В этом пункте угол вычисляется сложением и делением. Сначала берём угол за 5 минут — это \(30^\circ\). Потом добавляем половину этого угла, то есть делим 30 на 2, получаем 15. Суммируем: \(30 + \frac{30}{2} = 30 + 15 = 45^\circ\). Это означает, что стрелка прошла угол в 45 градусов, что соответствует 7,5 минутам.

Такой способ вычисления используется, когда нужно учесть нецелое количество интервалов, например, 7,5 минут, что равно 5 минутам плюс половина интервала.

г) Здесь сначала умножаем угол за 5 минут на 3: \(30 \cdot 3 = 90^\circ\), что соответствует 15 минутам. Затем прибавляем половину угла за 5 минут, то есть \( \frac{30}{2} = 15^\circ \). В итоге получаем сумму: \(90 + 15 = 105^\circ\). Это угол, пройденный стрелкой за 17,5 минут.

Такой расчёт показывает, как можно комбинировать целые и дробные интервалы времени для точного определения угла.

д) В этом случае умножаем угол за 5 минут на 4: \(30 \cdot 4 = 120^\circ\), что соответствует 20 минутам. Затем прибавляем половину угла за 5 минут, то есть \( \frac{30}{2} = 15^\circ \). Итоговый угол равен \(120 + 15 = 135^\circ\). Это угол, который стрелка проходит за 22,5 минуты.

Данный метод позволяет вычислять углы для времени, которое выражается в сумме целых и половинных интервалов по 5 минут, обеспечивая точность измерения.