ГДЗ по Математике 5 Класс Часть 2 Номер 1000 Мнемозина Виленкин, Жохов — Подробные Ответы

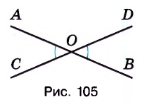
Прямые \(AB\) и \(CD\) (рис. 105) пересекаются в точке \(O\). Докажите, что углы \(AOC\) и \(BOD\) равны.

\( \angle AOB = \angle AOD + \angle BOD; \)
\( \angle COD = \angle AOC + \angle AOD. \)

Так как \( \angle AOB = \angle COD \), приравниваем правые части равенств:
\( \angle AOD + \angle BOD = \angle AOC + \angle AOD. \)

Угол \( \angle AOD \) одинаковый в левой и правой частях, сокращаем его.

Тогда:
\( \angle BOD = \angle AOC. \)

Что и требовалось доказать.

\( \angle AOB = \angle AOD + \angle BOD \) и \( \angle COD = \angle AOC + \angle AOD \) — это выражения, которые показывают, что угол \( \angle AOB \) можно представить как сумму двух углов \( \angle AOD \) и \( \angle BOD \), а угол \( \angle COD \) как сумму углов \( \angle AOC \) и \( \angle AOD \). Такое разложение углов происходит из-за того, что точка \( O \) является общей вершиной, а лучи \( OA \), \( OB \), \( OC \), \( OD \) формируют эти углы. Важно понимать, что углы \( \angle AOD \) в обоих равенствах совпадают, так как они имеют одну и ту же вершину и стороны.

Далее, в условии сказано, что \( \angle AOB = \angle COD \). Это значит, что сумма углов \( \angle AOD + \angle BOD \) равна сумме углов \( \angle AOC + \angle AOD \). Записывая это равенство, получаем: \( \angle AOD + \angle BOD = \angle AOC + \angle AOD \). Здесь мы видим, что угол \( \angle AOD \) встречается с обеих сторон уравнения. Поскольку углы равны, можно сократить одинаковый угол \( \angle AOD \) с обеих сторон, что позволяет упростить выражение.

После сокращения угла \( \angle AOD \) остается равенство \( \angle BOD = \angle AOC \). Это означает, что угол \( \angle BOD \) равен углу \( \angle AOC \), что и требовалось доказать. Таким образом, исходное равенство углов \( \angle AOB \) и \( \angle COD \) позволяет перейти к равенству углов \( \angle BOD \) и \( \angle AOC \) через разложение на части и сокращение одинакового угла. Этот приём широко используется в геометрии для доказательства равенства углов или отрезков путем разложения и упрощения выражений.