ГДЗ по Математике 5 Класс Часть 2 Номер 1 Мнемозина Виленкин, Жохов — Подробные Ответы

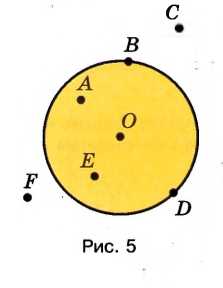
Какие из точек, отмеченных на рисунке 5:
а) лежат на окружности;
б) лежат внутри круга;
в) не лежат на окружности;
г) лежат вне круга?

а) Лежат на окружности точки \( B \) и \( D \).

б) Лежат внутри круга точки \( A \), \( O \) и \( E \).

в) Не лежат на окружности точки \( C \), \( F \), \( A \), \( O \) и \( E \).

г) Лежат вне круга точки \( C \) и \( F \).

а) Точки \( B \) и \( D \) лежат на окружности, что означает, что расстояние от каждой из этих точек до центра окружности равно радиусу этой окружности. Если обозначить центр окружности как \( O \), а радиус как \( R \), то для точек на окружности выполняется равенство \( OB = R \) и \( OD = R \). Это ключевое свойство окружности: все точки, расположенные на ней, находятся на одинаковом расстоянии от центра.

Таким образом, точки \( B \) и \( D \) принадлежат множеству точек, удовлетворяющих уравнению окружности \( (x — x_0)^2 + (y — y_0)^2 = R^2 \), где \( (x_0, y_0) \) — координаты центра \( O \). Это значит, что если измерить длину отрезков \( OB \) и \( OD \), то они будут равны радиусу \( R \).

б) Точки \( A \), \( O \) и \( E \) лежат внутри круга, что означает, что расстояние от этих точек до центра окружности меньше радиуса круга. Если центр круга обозначить \( O \), а радиус — \( R \), то для каждой из этих точек выполняется неравенство \( OA < R \), \( OO < R \) (где \( OO = 0 \), так как это центр), и \( OE < R \). Это условие указывает, что данные точки расположены в области, ограниченной окружностью, но не на самой окружности. В координатной форме это означает, что для точек внутри круга \( (x - x_0)^2 + (y - y_0)^2 < R^2 \). Таким образом, точки \( A \), \( O \) и \( E \) находятся строго внутри фигуры, не доходя до её границы. в) Точки \( C \), \( F \), \( A \), \( O \) и \( E \) не лежат на окружности, то есть расстояния от них до центра окружности не равны радиусу \( R \). Это можно записать как \( CO \neq R \), \( FO \neq R \), \( AO \neq R \), \( OO \neq R \), \( EO \neq R \). Из этого следует, что все эти точки либо лежат внутри круга, либо вне его, но не на границе. Для точек внутри круга выполняется \( d < R \), для точек вне круга — \( d > R \), где \( d \) — расстояние от точки до центра окружности. Таким образом, данные точки не принадлежат множеству точек, удовлетворяющих уравнению окружности, а находятся либо внутри, либо снаружи неё.

г) Точки \( C \) и \( F \) лежат вне круга, что означает, что расстояния от этих точек до центра окружности больше радиуса \( R \). Если центр окружности — \( O \), то для этих точек выполняется неравенство \( CO > R \) и \( FO > R \).

Это говорит о том, что точки находятся за пределами круга, то есть вне области, ограниченной окружностью. В координатной форме для таких точек верно \( (x — x_0)^2 + (y — y_0)^2 > R^2 \). Таким образом, точки \( C \) и \( F \) расположены на расстоянии, превышающем радиус круга, и не принадлежат ни окружности, ни её внутренней области.