ГДЗ по Математике 5 Класс Часть 2 Номер 1033 Мнемозина Виленкин, Жохов — Подробные Ответы

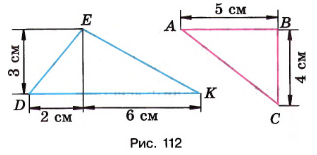
Дополните каждый треугольник, изображённый на рисунке 112, до прямоугольника и найдите площади треугольников.

Площадь прямоугольного треугольника равна половине площади прямоугольника.

\( S_{DEK} = \frac{2 \cdot 3}{2} + \frac{6 \cdot 3}{2} = \frac{6}{2} + \frac{18}{2} = 3 + 9 = 12 \ (\text{см}^2) \).

\( S_{ABC} = \frac{5 \cdot 4}{2} = \frac{20}{2} = 10 \ (\text{см}^2) \).

Ответ: \( S_{DEK} = 12 \ \text{см}^2; \quad S_{ABC} = 10 \ \text{см}^2 \).

Площадь прямоугольного треугольника равна половине площади прямоугольника, так как прямоугольный треугольник можно рассматривать как половину прямоугольника, если его гипотенуза совпадает с диагональю этого прямоугольника. Для вычисления площади треугольника нужно умножить длины двух его катетов и разделить результат на 2.

Рассмотрим сначала треугольник \( DEK \). Его катеты имеют длины 2 и 3, а другой прямоугольник — стороны 6 и 3. Площадь треугольника \( DEK \) находится как сумма половин площадей двух прямоугольников: \( \frac{2 \cdot 3}{2} \) и \( \frac{6 \cdot 3}{2} \). Это выражается формулой \( S_{DEK} = \frac{2 \cdot 3}{2} + \frac{6 \cdot 3}{2} \). Сначала вычисляем произведения: \( 2 \cdot 3 = 6 \) и \( 6 \cdot 3 = 18 \), затем делим каждое на 2, получая \( \frac{6}{2} = 3 \) и \( \frac{18}{2} = 9 \). Складывая эти результаты, имеем \( 3 + 9 = 12 \), что и является площадью треугольника \( DEK \) в квадратных сантиметрах.

Далее рассмотрим треугольник \( ABC \), у которого катеты равны 5 и 4. Площадь этого треугольника вычисляется по формуле \( S_{ABC} = \frac{5 \cdot 4}{2} \). Сначала умножаем \( 5 \) на \( 4 \), получая \( 20 \), затем делим на 2, что даёт \( 10 \). Таким образом, площадь треугольника \( ABC \) равна 10 квадратным сантиметрам. Итоговый ответ записывается как \( S_{DEK} = 12 \ \text{см}^2 \) и \( S_{ABC} = 10 \ \text{см}^2 \).