ГДЗ по Математике 5 Класс Часть 1 Задания для самопроверки Параграф 1 Мнемозина Виленкин, Жохов — Подробные Ответы

1. Выберите числа, которые являются натуральными,
а) 0; 6) 1; в) 10; г) 1; д) 375.
2. Укажите выражение, в котором число 49 307 представлено в виде суммы разрядных слагаемых.
а) 40 000 + 9000 + 300 + 7;
б) 49 000 + 300 + 7;
в) 49 000 + 307;
г) 40 000 + 9000 + 30 + 7;
д) 40 000 + 9000 + 307.
3. Установите соответствие между числом, записанным словами, и числом, записанным цифрами.
A. Тридцать пять миллионов сорок две тысячи семь
Б. Триста пятьдесят четыре тысячи двести семьдесят
B. Триста пять миллионов четыре тысячи двести семь
Г. Три миллиарда пятьсот четыре тысячи двадцать семь
1) 305 004 207
2) 3 000 504 027
3) 35 042 007
4) 354 270
4. Выберите правильную запись числа 3 млрд 57 млн 207 тыс.
а) 357 207 000;
б) 3 570 270 000;
в) 357 207;
г) 3 057 207 000;
д) 3 057 000 207.
5. Сравните:
а) 1 000 001 и 1 млн;
б) 999 999 999 и 1 млрд;
в) 1 млрд и 1000 млн.
6. Пользуясь рисунком, укажите номера верных утверждений.
а) Прямая EF не пересекает отрезок AB.
б) Луч ОК не пересекает прямую EF.
в) Прямая EF пересекает отрезок CD.
г) Луч ОК пересекает отрезок CD.
д) Луч ОК пересекает отрезок АВ.
7. Найдите периметр треугольника, стороны которого равны 2 дм 3 мм, 12 см и 9 см 7 мм.
8. Укажите единицы длины, которые могут соответствовать:
а) толщине учебника 1) 55 км
б) длине комнаты 2) 535 см
в) росту человека 3) 540 м
г) расстоянию между городами 4) 2 см
д) высоте Останкинской башни 5) 154 см
9. Используя рисунок, запишите координаты точек А, В, С, D.
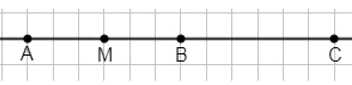
10. Точка М лежит между точками А и С, а точка В — между точками М и С. Какой из отрезков АС, АВ, ВM, МС имеет наименьшую длину?

№ 1.

а) \(0\) не натуральное (натуральные числа начинаются с \(1\)).
б) \(1\) натуральное.
в) \(10\) натуральное.
г) \(\frac{1}{2}\) не натуральное (не целое).
д) \(375\) натуральное.

Ответ: б), в), д).

№ 2.

\(49\,307 = 40\,000 + 9\,000 + 300 + 7\), значит верно разложение под буквой а).

Ответ: а).

№ 3.

\(35\,042\,007\) соответствует варианту 3).
\(354\,270\) соответствует варианту 4).
\(305\,004\,207\) соответствует варианту 1).
\(3\,000\,504\,027\) соответствует варианту 2).

Ответ: А ⇔ 3; Б ⇔ 4; В ⇔ 1; Г ⇔ 2.

№ 4.

\(3\) млрд \(57\) млн \(207\) тыс. \(= 3\,057\,207\,000\), это вариант г).

Ответ: г).

№ 5.

а) \(1\,000\,001 > 1\) млн, так как \(1\) млн \(= 1\,000\,000\).

б) \(999\,999\,999 < 1\) млрд, так как \(1\) млрд \(= 1\,000\,000\,000\).

в) \(1\) млрд \(= 1000\) млн, так как \(1\) млрд \(= 1\,000\,000\,000\) и \(1000\) млн \(= 1\,000\,000\,000\).

№ 6.

а) Прямая \(EF\) не пересекает отрезок \(AB\) — верно.
б) Луч \(OK\) не пересекает прямую \(EF\) — неверно.
в) Прямая \(EF\) пересекает отрезок \(CD\) — верно.
г) Луч \(OK\) пересекает отрезок \(CD\) — неверно.
д) Луч \(OK\) пересекает отрезок \(AB\) — верно.

Ответ: а), в), д).

№ 7.

\(2\) дм \(3\) мм \(= 20\) см \(3\) мм \(= 200\) мм \(3\) мм \(= 203\) мм.
\(12\) см \(= 120\) мм.
\(9\) см \(7\) мм \(= 97\) мм.

Периметр: \(203 + 120 + 97 = 420\) мм \(= 42\) см \(= 4\) дм \(2\) см.

Ответ: \(4\) дм \(2\) см.

№ 8.

а) толщина учебника ⇒ \(4)\) \(2\) см.
б) длина комнаты ⇒ \(2)\) \(535\) см.
в) рост человека ⇒ \(5)\) \(154\) см.
г) расстояние между городами ⇒ \(1)\) \(55\) км.
д) высота Останкинской башни ⇒ \(3)\) \(540\) м.

№ 9.

Единичный отрезок — одна клетка, поэтому: \(A(3)\), \(B(6)\), \(C(7)\), \(D(11)\).

№ 10.

По рисунку точки \(A\), \(M\), \(B\), \(C\) расположены так, что самый короткий из \(AC\), \(AB\), \(BM\), \(MC\) — \(BM\).

Ответ: \(BM\).

№ 1.

а) Натуральные числа в школьном курсе понимаются как числа для счета: \(1, 2, 3, 4, \ldots\). Число \(0\) к ним не относят, потому что оно не обозначает количество предметов при счете «один, два, три…».

Поэтому утверждение «\(0\) — натуральное число» неверно, а правильная оценка для \(0\): не является натуральным числом.

б) Число \(1\) — это первое число, с которого начинается счет. Оно относится к множеству натуральных чисел, так как является положительным целым числом.

Следовательно, утверждение «\(1\) — натуральное число» верно.

в) Число \(10\) — целое и положительное. Любое положительное целое число (включая двузначные, трехзначные и т.д.) является натуральным.

Значит, утверждение «\(10\) — натуральное число» верно.

г) Число \(\frac{1}{2}\) — это дробь, то есть не целое число. Натуральные числа должны быть целыми, поэтому дробные значения к ним не относятся.

Следовательно, утверждение «\(\frac{1}{2}\) — натуральное число» неверно, и правильный вывод: \(\frac{1}{2}\) не является натуральным числом.

д) Число \(375\) — целое и положительное. Натуральные числа включают любые положительные целые, независимо от того, насколько они большие.

Значит, утверждение «\(375\) — натуральное число» верно.

Ответ: б), в), д).

№ 2.

Чтобы разложить число \(49\,307\) на разрядные слагаемые, выделяем десятки тысяч, тысячи, сотни, десятки и единицы. В числе \(49\,307\) цифра \(4\) стоит в разряде десятков тысяч, цифра \(9\) — в разряде тысяч, \(3\) — в разряде сотен, \(0\) — в разряде десятков, \(7\) — в разряде единиц.

Поэтому разложение получается таким: \(49\,307 = 40\,000 + 9\,000 + 300 + 7\). Слагаемое для десятков отсутствует, потому что десятков \(0\), и добавлять \(0\) в виде отдельного слагаемого не требуется.

Значит, верный вариант — а).

Ответ: а).

№ 3.

A. Число \(35\,042\,007\) читается как «тридцать пять миллионов сорок две тысячи семь». Здесь миллионы равны \(35\), тысячи равны \(42\), единицы равны \(7\), поэтому запись должна соответствовать варианту, где именно такая структура: \(35\) млн, \(42\) тыс., \(7\).

Сопоставление дает: A соответствует \(3)\), потому что именно там указано число с миллионами \(35\), тысячами \(42\) и единицами \(7\).

Б. Число \(354\,270\) состоит из \(354\) тысяч и \(270\) единиц. Это означает: сотни тысяч \(3\), десятки тысяч \(5\), тысячи \(4\), сотни \(2\), десятки \(7\), единицы \(0\).

Поэтому Б соответствует \(4)\), так как в этом варианте записано именно \(354\,270\).

В. Число \(305\,004\,207\) удобно группировать по три цифры: \(305\) млн, \(004\) тыс., \(207\). Это означает, что тысяч ровно \(4\) (то есть \(4\,000\)), а затем \(207\).

Значит, В соответствует \(1)\), потому что там дано число \(305\,004\,207\) с нулем десятков тысяч и нулем тысяч в середине группы \(004\).

Г. Число \(3\,000\,504\,027\) — это \(3\) миллиарда \(000\) миллионов \(504\) тысячи \(027\). Здесь важно, что миллионы равны \(0\), поэтому группа миллионов записана как \(000\), а тысячи равны \(504\).

Следовательно, Г соответствует \(2)\), так как в этом варианте стоит число \(3\,000\,504\,027\).

Ответ: А ⇔ 3; Б ⇔ 4; В ⇔ 1; Г ⇔ 2.

№ 4.

Запись «\(3\) млрд \(57\) млн \(207\) тыс.» переводим в обычное число, учитывая значения разрядных единиц: \(1\) млрд \(= 1\,000\,000\,000\), \(1\) млн \(= 1\,000\,000\), \(1\) тыс. \(= 1\,000\). Тогда \(3\) млрд — это \(3\,000\,000\,000\), \(57\) млн — это \(57\,000\,000\), \(207\) тыс. — это \(207\,000\).

Складываем полученные части: \(3\,000\,000\,000 + 57\,000\,000 + 207\,000 = 3\,057\,207\,000\). Именно так получается полная запись данного числа без слов.

Следовательно, верный вариант — г).

Ответ: г).

№ 5.

а) Число \(1\,000\,001\) сравниваем с \(1\) млн, сначала переводя запись «миллион» в обычное число: \(1\) млн \(= 1\,000\,000\). Это одна и та же величина, просто записанная разными способами.

Далее сопоставляем разряды: \(1\,000\,001\) отличается от \(1\,000\,000\) на единицу, то есть \(1\,000\,001 = 1\,000\,000 + 1\). Поскольку добавили \(1\), получаем, что \(1\,000\,001 > 1\) млн.

б) Число \(999\,999\,999\) сравниваем с \(1\) млрд, переводя «миллиард» в число: \(1\) млрд \(= 1\,000\,000\,000\). Это базовый ориентир для сравнения: миллиард — это единица с девятью нулями.

Теперь видно, что \(999\,999\,999\) — это число на \(1\) меньше, чем \(1\,000\,000\,000\), то есть \(999\,999\,999 = 1\,000\,000\,000 — 1\). Если из числа вычесть \(1\), оно станет меньше исходного, значит \(999\,999\,999 < 1\) млрд.

в) Чтобы сравнить «\(1\) млрд» и «\(1000\) млн», переводим обе записи в одинаковую числовую форму. Известно, что \(1\) млрд \(= 1\,000\,000\,000\), то есть один миллиард — это тысяча миллионов, записанных одним числом.

Далее считаем, чему равны \(1000\) млн: так как \(1\) млн \(= 1\,000\,000\), то \(1000\) млн \(= 1000 \cdot 1\,000\,000 = 1\,000\,000\,000\). Оба выражения дают одно и то же число \(1\,000\,000\,000\), поэтому \(1\) млрд \(= 1000\) млн.

№ 6.

а) Проверяется факт пересечения: пересечь отрезок \(AB\) значит иметь с ним хотя бы одну общую точку. По рисунку прямая \(EF\) проходит так, что общих точек с отрезком \(AB\) у нее нет.

Поэтому утверждение «прямая \(EF\) не пересекает отрезок \(AB\)» является верным.

б) Здесь речь о луче \(OK\) и прямой \(EF\). По рисунку луч направлен так, что при продолжении от точки \(O\) он все же встречается с прямой \(EF\), то есть имеет с ней общую точку.

Значит, утверждение «луч \(OK\) не пересекает прямую \(EF\)» неверно.

в) Пересечение прямой с отрезком \(CD\) означает, что прямая проходит через отрезок и имеет с ним общую точку. На рисунке видно, что линия \(EF\) пересекает отрезок \(CD\).

Следовательно, утверждение «прямая \(EF\) пересекает отрезок \(CD\)» верно.

г) Утверждение говорит, что луч \(OK\) пересекает отрезок \(CD\). По рисунку направление луча и положение отрезка \(CD\) таковы, что луч до отрезка не доходит и общей точки с \(CD\) не имеет.

Поэтому утверждение «луч \(OK\) пересекает отрезок \(CD\)» неверно.

д) Здесь нужно определить, есть ли общая точка у луча \(OK\) и отрезка \(AB\). По рисунку луч \(OK\) проходит через отрезок \(AB\), то есть пересекает его.

Следовательно, утверждение «луч \(OK\) пересекает отрезок \(AB\)» верно.

Ответ: а), в), д).

№ 7.

Сначала приводим все стороны треугольника к одним и тем же единицам, удобнее всего к миллиметрам. \(2\) дм \(3\) мм это \(20\) см \(3\) мм, а \(20\) см \(= 200\) мм, значит получаем \(200\) мм \(+ 3\) мм \(= 203\) мм.

Далее: \(12\) см \(= 120\) мм, потому что \(1\) см \(= 10\) мм. И \(9\) см \(7\) мм это \(90\) мм \(+ 7\) мм \(= 97\) мм.

Теперь периметр — сумма всех трех сторон: \(203 + 120 + 97 = 420\) мм. Переводим обратно: \(420\) мм \(= 42\) см, так как \(10\) мм \(= 1\) см, а \(42\) см \(= 4\) дм \(2\) см, потому что \(1\) дм \(= 10\) см.

Ответ: \(4\) дм \(2\) см.

№ 8.

а) Толщина учебника — это маленькая величина, обычно измеряется в сантиметрах. Из предложенных вариантов подходит \(2\) см, потому что это реалистичная толщина книги.

Поэтому сопоставление такое: толщина учебника ⇒ \(4)\) \(2\) см.

б) Длина комнаты — величина больше метра, часто несколько метров. В сантиметрах типичное значение порядка нескольких сотен сантиметров, например \(535\) см, что равно \(5\) м \(35\) см.

Значит: длина комнаты ⇒ \(2)\) \(535\) см.

в) Рост человека обычно около \(150\)–\(180\) см для взрослого. Среди вариантов подходит \(154\) см, это нормальное значение роста.

Следовательно: рост человека ⇒ \(5)\) \(154\) см.

г) Расстояние между городами измеряют в километрах, потому что это большие расстояния. Вариант \(55\) км соответствует реальному расстоянию между близкими городами.

Поэтому: расстояние между городами ⇒ \(1)\) \(55\) км.

д) Высота Останкинской башни измеряется в метрах, и это сотни метров. Подходит \(540\) м как реальная величина для телебашни.

Значит: высота Останкинской башни ⇒ \(3)\) \(540\) м.

№ 9.

Сказано, что единичный отрезок равен одной клетке тетради, то есть шаг по координатной прямой соответствует перемещению на одну клетку. Поэтому координата точки — это количество таких шагов от начала отсчета до точки.

По рисунку точки стоят на соответствующих делениях: \(A\) на \(3\), \(B\) на \(6\), \(C\) на \(7\), \(D\) на \(11\). Это записывается так: \(A(3)\), \(B(6)\), \(C(7)\), \(D(11)\).

№ 10.

По рисунку точки на прямой расположены в порядке \(A\), затем \(M\), затем \(B\), затем \(C\). Длины отрезков на координатной сетке удобно сравнивать по числу клеток между точками: чем меньше промежуток, тем короче отрезок.

Отрезок \(BM\) соединяет соседние точки \(B\) и \(M\), и расстояние между ними на рисунке самое маленькое по сравнению с промежутками \(AB\), \(MC\) и особенно \(AC\). Поэтому среди \(AC\), \(AB\), \(BM\), \(MC\) наименьшую длину имеет именно \(BM\).

Ответ: \(BM\).