ГДЗ по Математике 5 Класс Часть 1 Номер 833 Мнемозина Виленкин, Жохов — Подробные Ответы

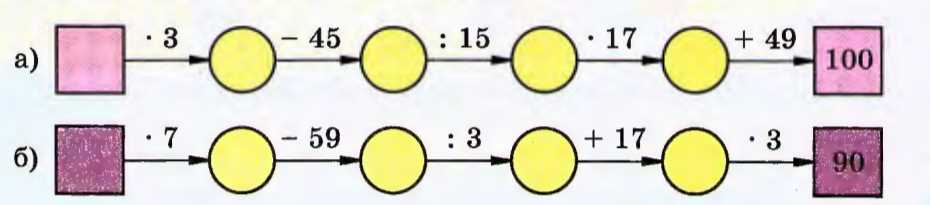
Восстановите цепочку вычислений:

а) Выполним обратные действия:
\(100 — 49 = 51\);
\(51 : 17 = 3\);
\(3 \cdot 15 = 45\);
\(45 + 45 = 90\);
\(90 : 3 = 30\).

Тогда:
\(30 \cdot 3 = 90 — 45 = 45 : 15 = 3 \cdot 17 = 51 + 49 = 100\).

б) Выполним обратные действия:
\(90 : 3 = 30\);
\(30 — 17 = 13\);
\(13 \cdot 3 = 39\);
\(39 + 59 = 98\);
\(98 : 7 = 14\).

Тогда:
\(14 \cdot 7 = 98 — 59 = 39 : 3 = 13 + 17 = 30 \cdot 3 = 90\).

а) В этом задании нам нужно выполнить обратные арифметические действия, чтобы проверить правильность выражения и понять, как связаны между собой числа. Сначала вычисляем разность \(100 — 49\), что даёт нам \(51\). Это действие показывает, каким числом нужно было бы дополнить \(49\), чтобы получить \(100\). Далее делим \(51\) на \(17\), получая результат \(3\), что означает, что \(51\) можно разбить на \(17\) частей по \(3\) в каждой. Следующий шаг — умножение \(3\) на \(15\), что даёт \(45\). Это действие позволяет понять, как из меньших частей можно составить большее число. Потом складываем \(45 + 45\), получая \(90\), что показывает удвоение значения \(45\). И, наконец, делим \(90\) на \(3\), получая \(30\), что служит проверкой правильности предыдущих действий.

Во второй части этого пункта мы используем полученные результаты для подтверждения исходного выражения. Начинаем с умножения \(30 \cdot 3\), что возвращает нас к числу \(90\). Затем вычитаем \(45\), получая \(45\). Делим \(45\) на \(15\), что даёт \(3\), и умножаем \(3\) на \(17\), получая \(51\). В конце прибавляем \(49\), что возвращает исходное число \(100\). Таким образом, последовательность обратных действий подтверждает правильность исходного выражения и показывает взаимосвязь между числами.

б) В этой части также выполняются обратные действия для проверки и понимания арифметических операций. Сначала делим \(90\) на \(3\), получая \(30\). Это действие показывает, что \(90\) можно разбить на три равные части по \(30\). Затем из \(30\) вычитаем \(17\), получая \(13\), что иллюстрирует уменьшение числа на заданное значение. После этого умножаем \(13\) на \(3\), получая \(39\), что показывает, как число увеличивается при умножении. К результату \(39\) прибавляем \(59\), получая \(98\), и делим \(98\) на \(7\), что даёт \(14\), демонстрируя разбиение числа на несколько частей.

Далее мы проверяем исходное выражение, используя полученные результаты. Умножаем \(14\) на \(7\), получая \(98\), затем вычитаем \(59\), что даёт \(39\). Делим \(39\) на \(3\), получая \(13\), прибавляем \(17\), получая \(30\), умножаем \(30\) на \(3\), что возвращает нас к числу \(90\). Такая последовательность действий доказывает правильность вычислений и взаимосвязь всех чисел в выражении.