ГДЗ по Математике 5 Класс Часть 1 Номер 832 Мнемозина Виленкин, Жохов — Подробные Ответы

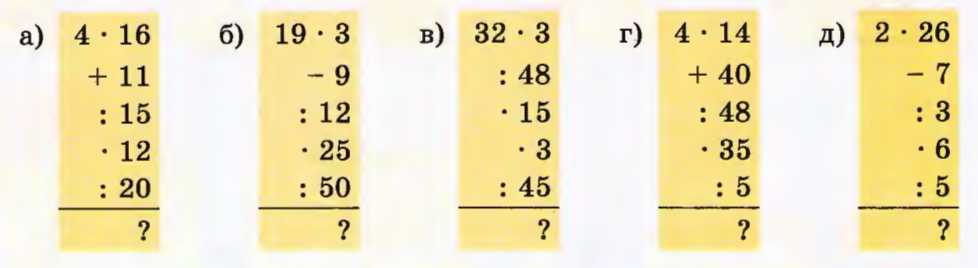
Вычислите устно:

а) \(4 \cdot 16 = 64\);
\(64 + 11 = 75\);
\(75 : 15 = 5\);
\(5 \cdot 12 = 60\);
\(60 : 20 = 3\).

б) \(19 \cdot 3 = 57\);
\(57 — 9 = 48\);
\(48 : 12 = 4\);
\(4 \cdot 25 = 100\);
\(100 : 50 = 2\).

в) \(32 \cdot 3 = 96\);
\(96 : 48 = 2\);
\(2 \cdot 15 = 30\);
\(30 \cdot 3 = 90\);
\(90 : 45 = 2\).

г) \(4 \cdot 14 = 56\);
\(56 + 40 = 96\);
\(96 : 48 = 2\);
\(2 \cdot 35 = 70\);
\(70 : 5 = 14\).

д) \(2 \cdot 26 = 52\);
\(52 — 7 = 45\);
\(45 : 3 = 15\);
\(15 \cdot 6 = 90\);
\(90 : 5 = 18\).

а) Сначала умножаем числа \(4\) и \(16\), получая произведение \(64\), то есть \(4 \cdot 16 = 64\). Это базовая операция умножения, где мы увеличиваем число \(4\) в \(16\) раз. Далее к результату прибавляем \(11\), что даёт \(64 + 11 = 75\). Здесь мы применяем сложение, увеличивая сумму на \(11\), что является простым арифметическим действием. Следующий шаг — деление числа \(75\) на \(15\), что равно \(5\), то есть \(75 : 15 = 5\). Деление показывает, сколько раз число \(15\) содержится в \(75\). После этого умножаем \(5\) на \(12\), получая \(60\), то есть \(5 \cdot 12 = 60\). Здесь мы увеличиваем число \(5\) в \(12\) раз. Последнее действие — деление \(60\) на \(20\), что даёт \(3\), то есть \(60 : 20 = 3\). Это показывает, сколько раз число \(20\) помещается в \(60\).

б) Начинаем с умножения \(19\) на \(3\), получая \(57\), то есть \(19 \cdot 3 = 57\). Это стандартное умножение, где число \(19\) увеличивается в \(3\) раза. Затем из результата вычитаем \(9\), получая \(48\), то есть \(57 — 9 = 48\). Вычитание уменьшает число на заданную величину. После этого делим \(48\) на \(12\), что равно \(4\), то есть \(48 : 12 = 4\). Деление показывает, сколько раз \(12\) входит в \(48\). Далее умножаем \(4\) на \(25\), получая \(100\), то есть \(4 \cdot 25 = 100\). Здесь число \(4\) увеличивается в \(25\) раз. В конце делим \(100\) на \(50\), что даёт \(2\), то есть \(100 : 50 = 2\), показывая, сколько раз \(50\) содержится в \(100\).

в) Сначала умножаем \(32\) на \(3\), получая \(96\), то есть \(32 \cdot 3 = 96\). Это стандартная операция умножения. Затем делим \(96\) на \(48\), что даёт \(2\), то есть \(96 : 48 = 2\). Деление показывает, сколько раз число \(48\) помещается в \(96\). После этого умножаем \(2\) на \(15\), получая \(30\), то есть \(2 \cdot 15 = 30\). Умножение увеличивает число в \(15\) раз. Далее умножаем \(30\) на \(3\), получая \(90\), то есть \(30 \cdot 3 = 90\). Это ещё одно умножение, увеличивающее число. В конце делим \(90\) на \(45\), что равно \(2\), то есть \(90 : 45 = 2\), показывая, сколько раз \(45\) входит в \(90\).

г) Сначала умножаем \(4\) на \(14\), получая \(56\), то есть \(4 \cdot 14 = 56\). Это простое умножение. Затем прибавляем к \(56\) число \(40\), получая \(96\), то есть \(56 + 40 = 96\). Сложение увеличивает сумму. Далее делим \(96\) на \(48\), что даёт \(2\), то есть \(96 : 48 = 2\). Деление показывает, сколько раз \(48\) содержится в \(96\). После этого умножаем \(2\) на \(35\), получая \(70\), то есть \(2 \cdot 35 = 70\). Умножение увеличивает число в \(35\) раз. Последнее действие — деление \(70\) на \(5\), что даёт \(14\), то есть \(70 : 5 = 14\). Это показывает, сколько раз \(5\) помещается в \(70\).

д) Начинаем с умножения \(2\) на \(26\), получая \(52\), то есть \(2 \cdot 26 = 52\). Это базовая операция умножения. Затем вычитаем из \(52\) число \(7\), получая \(45\), то есть \(52 — 7 = 45\). Вычитание уменьшает число на заданную величину. Далее делим \(45\) на \(3\), что равно \(15\), то есть \(45 : 3 = 15\). Деление показывает, сколько раз \(3\) содержится в \(45\). После этого умножаем \(15\) на \(6\), получая \(90\), то есть \(15 \cdot 6 = 90\). Умножение увеличивает число в \(6\) раз. В конце делим \(90\) на \(5\), что даёт \(18\), то есть \(90 : 5 = 18\), показывая, сколько раз \(5\) помещается в \(90\).