ГДЗ по Математике 5 Класс Часть 1 Номер 779 Мнемозина Виленкин, Жохов — Подробные Ответы

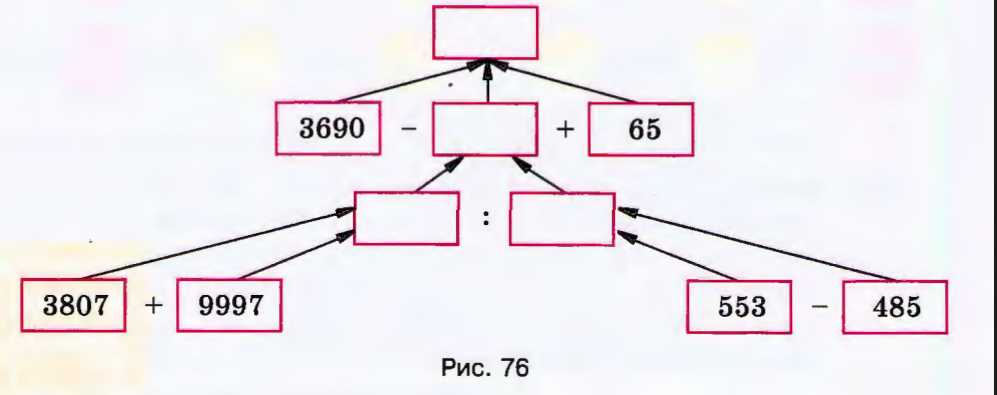
Составьте выражение по схеме и найдите его значение (рис. 76).

\(3690 — (3807 + 9997) : (553 — 485) + 65\)

1) \(3807 + 9997 = 13804\);

2) \(553 — 485 = 68\);

3) \(13804 : 68 = 203\);

4) \(3690 — 203 = 3487\);

5) \(3487 + 65 = 3552\).

\(3690 — (3807 + 9997) : (553 — 485) + 65\)

1) Сначала выполняем действие в первых скобках, потому что по порядку действий скобки считаются раньше деления и вычитания. Складываем числа внутри скобок: \(3807 + 9997\).

Получаем \(3807 + 9997 = 13804\), то есть выражение принимает вид \(3690 — 13804 : (553 — 485) + 65\).

2) Далее выполняем действие во вторых скобках, потому что это тоже приоритетный шаг перед делением. Находим разность: \(553 — 485\).

Имеем \(553 — 485 = 68\), после этого выражение упрощается до \(3690 — 13804 : 68 + 65\).

3) Теперь выполняем деление, так как деление выполняется раньше, чем сложение и вычитание в оставшейся части выражения. Делим \(13804\) на \(68\): \(13804 : 68\).

Получаем \(13804 : 68 = 203\), значит выражение становится \(3690 — 203 + 65\).

4) Далее выполняем вычитание слева направо среди оставшихся действий сложения и вычитания. Находим разность \(3690 — 203\), чтобы перейти к последнему шагу.

Итак, \(3690 — 203 = 3487\), после этого остаётся прибавить \(65\): \(3487 + 65\).

5) В конце выполняем сложение, так как других действий уже нет. Считаем \(3487 + 65\), что завершает вычисление исходного выражения.

Получаем \(3487 + 65 = 3552\).