ГДЗ по Математике 5 Класс Часть 1 Номер 775 Мнемозина Виленкин, Жохов — Подробные Ответы

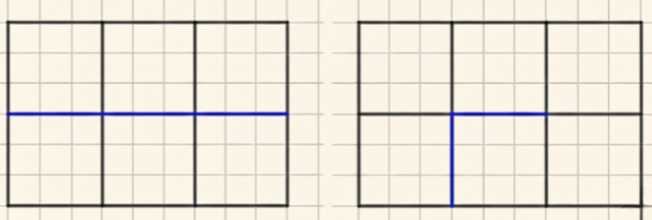
Сколько квадратов изображено на рисунке 75? Какие из них равны между собой? Разделите прямоугольник на две равные части, каждая из которых состоит из целых квадратов, двумя способами.

Пусть площадь каждого из равных квадратов \(MABK, KBCP, PCDT, XMKS, SKPY, YPTE\) равна \(s\), а площадь квадратов \(XACY\) и \(SBDE\) равна \(S\).

При разрезании прямоугольника линией \(MT\) (или линией \(SKPC\)) в каждой из двух частей оказывается по три квадрата площади \(s\), а каждый из квадратов площади \(S\) делится разрезом пополам, то есть даёт в каждую часть по \(\frac{S}{2}\).

Следовательно, площадь каждой части равна \(3s+\frac{S}{2}+\frac{S}{2}=3s+S\), значит прямоугольник разделён на две равные части.

Пусть площадь каждого из шести равных квадратов \(MABK, KBCP, PCDT, XMKS, SKPY, YPTE\) одинакова и равна \(s\). Это удобно, потому что тогда вклад каждого такого квадрата в площадь любой части рисунка можно считать одинаковыми «порциями» площади \(s\). Аналогично, квадраты \(XACY\) и \(SBDE\) равны между собой, значит их площади одинаковы; обозначим площадь каждого из них через \(S\).

Смысл разрезания прямоугольника линией \(MT\) (или линией \(SKPC\)) в том, что мы делим весь большой прямоугольник на две фигуры и сравниваем их площади через то, из каких частей они «собраны». На рисунке видно, что внутри прямоугольника есть 8 квадратов, и разрез проходит так, что некоторые квадраты целиком оказываются в одной части, а некоторые пересекаются разрезом и делятся между частями.

Рассмотрим сначала шесть малых равных квадратов площади \(s\). По расположению на схеме при разрезе каждая из двух получившихся частей содержит по три таких квадрата целиком. Значит, вклад малых квадратов в площадь каждой части равен \(3s\), и этот вклад в обеих частях одинаков, потому что количество целых квадратов \(s\) по обе стороны разреза совпадает.

Теперь посмотрим на два больших равных квадрата \(XACY\) и \(SBDE\) площади \(S\). Линия разреза в обоих вариантах проходит через каждый из этих квадратов так, что делит его на две равновеликие части (на рисунке это отражено симметричным пересечением квадрата линией разреза). Поэтому от квадрата площади \(S\) в каждую из двух частей попадает ровно половина его площади, то есть \(\frac{S}{2}\). Поскольку таких квадратов два и каждый делится пополам, суммарный вклад от этих двух квадратов в каждую часть равен \(\frac{S}{2}+\frac{S}{2}=S\).

Итак, площадь первой части складывается из площади трёх малых квадратов и долей от двух больших квадратов: \(3s+\frac{S}{2}+\frac{S}{2}=3s+S\). Точно так же площадь второй части, по тем же причинам (три целых малых квадрата и половины от каждого из двух больших), равна \(3s+\frac{S}{2}+\frac{S}{2}=3s+S\).

Следовательно, обе части имеют одинаковую площадь \(3s+S\). Значит, разрез линией \(MT\) (или линией \(SKPC\)) действительно делит исходный прямоугольник на две равные по площади части.