ГДЗ по Математике 5 Класс Часть 1 Номер 767 Мнемозина Виленкин, Жохов — Подробные Ответы

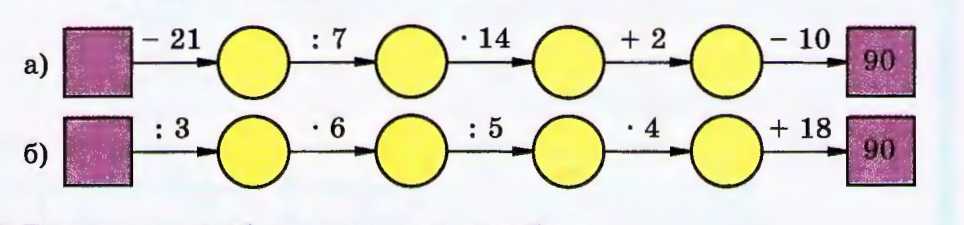
Восстановите цепочку вычислений:

а) Обратные действия: \(90+10=100\), \(100-2=98\), \(98:14=7\), \(7\cdot7=49\), \(49+21=70\).

Тогда: \(70-21=49\), \(49:7=7\), \(7\cdot14=98\), \(98+2=100\), \(100-10=90\).

б) Обратные действия: \(90-18=72\), \(72:4=18\), \(18\cdot5=90\), \(90:6=15\), \(15\cdot3=45\).

Тогда: \(45:3=15\), \(15\cdot6=90\), \(90:5=18\), \(18\cdot4=72\), \(72+18=90\).

а) Здесь дан результат всей цепочки действий, и нужно восстановить исходное число, выполняя обратные операции в обратном порядке. Сначала смотрим на самый последний шаг: к числу прибавили \(21\) и получили \(70\), значит перед этим было \(70-21=49\). Это возвращает нас на один шаг назад, потому что вычитание — обратное действие к сложению.

Далее видим, что перед сложением было умножение: \(7\cdot7=49\). Чтобы вернуться к числу \(7\), нужно выполнить действие, обратное умножению на \(7\), то есть разделить на \(7\): \(49:7=7\). Затем выполнялось деление \(98:14=7\), поэтому обратное действие — умножить на \(14\): \(7\cdot14=98\). Так мы восстанавливаем число, которое стояло до деления.

После этого по цепочке шло вычитание \(100-2=98\), значит обратное действие — прибавить \(2\): \(98+2=100\). И самый первый переход был сложением \(90+10=100\), поэтому возвращаемся вычитанием \(10\): \(100-10=90\). Вся обратная цепочка записывается так: \(70-21=49\), \(49:7=7\), \(7\cdot14=98\), \(98+2=100\), \(100-10=90\).

б) Аналогично, нужно восстановить исходное число, последовательно отменяя сделанные действия в обратном порядке. В данной цепочке известен исходный ориентир \(90\), и показано, как из него получали промежуточные значения: \(90-18=72\), затем \(72:4=18\), затем \(18\cdot5=90\), затем \(90:6=15\), затем \(15\cdot3=45\). Чтобы проверочно «вернуться» назад от конечного числа \(45\) к исходному \(90\), выполняем обратные операции: если последним было умножение на \(3\), то отменяем его делением на \(3\).

Поэтому сначала \(45:3=15\). До этого выполнялось деление на \(6\) (получили \(15\)), значит обратное действие — умножить на \(6\): \(15\cdot6=90\). Раньше было умножение на \(5\), значит обратное — разделить на \(5\): \(90:5=18\). Это восстанавливает число \(18\), которое появилось после деления на \(4\).

Дальше отменяем деление на \(4\) умножением на \(4\): \(18\cdot4=72\). И самый первый шаг цепочки был вычитанием \(18\) из \(90\), поэтому обратное действие — прибавить \(18\): \(72+18=90\). Итоговая обратная цепочка совпадает с образцом: \(45:3=15\), \(15\cdot6=90\), \(90:5=18\), \(18\cdot4=72\), \(72+18=90\).