ГДЗ по Математике 5 Класс Часть 1 Номер 742 Мнемозина Виленкин, Жохов — Подробные Ответы

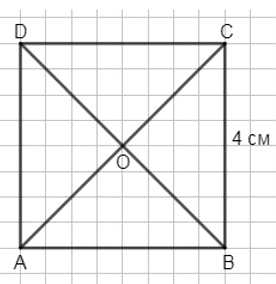
Постройте квадрат \(ABCD\) со стороной 4 см и проведите в нём отрезки \(AC\) и \(BD\). Чему равна площадь каждого из четырёх получившихся треугольников?
Сложите из двух таких треугольников новый квадрат. Чему равна его площадь?

Площадь треугольников \(COD\), \(COB\), \(AOB\), \(AOD\) равна четвертой части площади квадрата.
\(S_{\triangle COD} = S_{\triangle COB} = S_{\triangle AOB} = S_{\triangle AOD} = \frac{a^2}{4} = \frac{4^2}{4} = \frac{16}{4} = 4 \text{ (см}^2)\).

Сложим из двух треугольников новый квадрат.
Площадь получившегося квадрата равна половине площади квадрата \(ABCD\) или удвоенной площади маленького треугольника.
\(S = \frac{a^2}{2} = \frac{4^2}{2} = \frac{16}{2} = 8 \text{ (см}^2)\).

Ответ:
\(S_{\triangle COD} = S_{\triangle COB} = S_{\triangle AOB} = S_{\triangle AOD} = 4 \text{ см}^2\);
\(S_{\text{квад.}} = 8 \text{ см}^2\).

Площадь квадрата \(ABCD\) равна \(a^2\), где \(a = 4 \text{ см}\). Точки \(O\) — это точка пересечения диагоналей квадрата, которые делят квадрат на четыре равных треугольника: \(COD\), \(COB\), \(AOB\), \(AOD\). Поскольку диагонали квадрата равны и пересекаются под прямым углом, каждая из этих четырех частей имеет одинаковую площадь. Следовательно, площадь каждого треугольника равна четвертой части площади квадрата. Запишем это как \(S_{\triangle COD} = S_{\triangle COB} = S_{\triangle AOB} = S_{\triangle AOD} = \frac{a^2}{4}\).

Подставляя значение \(a = 4\), получаем \(S_{\triangle COD} = \frac{4^2}{4} = \frac{16}{4} = 4 \text{ см}^2\). Таким образом, каждый из четырех треугольников имеет площадь 4 квадратных сантиметра. Это объясняется тем, что диагонали квадрата делят его на четыре равных по площади треугольника, так как диагонали равны и пересекаются в серединах друг друга, а площадь квадрата — это площадь, из которой эти треугольники составляют равные части.

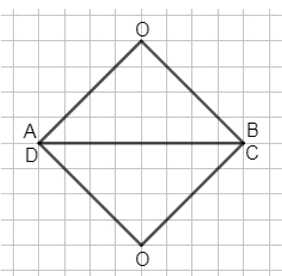
Если сложить два таких треугольника, например \(COD\) и \(COB\), получится новый квадрат, как показано на втором рисунке. Площадь этого нового квадрата будет равна сумме площадей двух маленьких треугольников. Поскольку площадь каждого треугольника равна \(4 \text{ см}^2\), площадь нового квадрата равна \(8 \text{ см}^2\). Это также можно выразить через площадь исходного квадрата \(ABCD\), так как площадь нового квадрата равна половине площади квадрата \(ABCD\), то есть \(S = \frac{a^2}{2}\).

Подставляем \(a = 4\) и вычисляем площадь нового квадрата: \(S = \frac{4^2}{2} = \frac{16}{2} = 8 \text{ см}^2\). Таким образом, площадь нового квадрата, составленного из двух треугольников, равна 8 квадратных сантиметров, что в два раза больше площади одного из маленьких треугольников и в два раза меньше площади исходного квадрата \(ABCD\). Это объясняется геометрией построения и свойствами диагоналей квадрата.