ГДЗ по Математике 5 Класс Часть 1 Номер 741 Мнемозина Виленкин, Жохов — Подробные Ответы

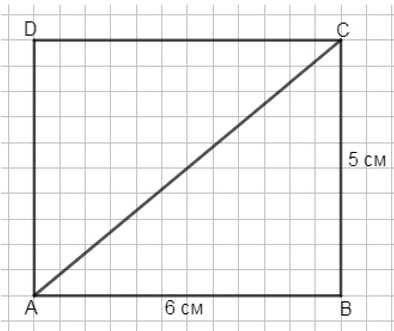
Начертите прямоугольник \(ABCD\), соедините отрезком вершины \(A\) и \(C\). Найдите площади треугольников \(ABC\) и \(ACD\), если \(AB = 6\) см и \(BC = 5\) см.

Площадь прямоугольника \( ABCD \) равна произведению сторон: \( AB \cdot BC = 6 \cdot 5 = 30 \, \text{см}^2 \).

Площадь треугольников \( ABC \) и \( ACD \) равна половине площади прямоугольника, так как диагональ делит прямоугольник на два равных треугольника.

Следовательно, площадь каждого треугольника:
\( S_{\triangle ABC} = S_{\triangle ACD} = \frac{AB \cdot BC}{2} = \frac{30}{2} = 15 \, \text{см}^2 \).

Ответ: \( S_{\triangle ABC} = S_{\triangle ACD} = 15 \, \text{см}^2 \).

Площадь прямоугольника \( ABCD \) вычисляется как произведение длины и ширины. В данном случае длина \( AB \) равна 6 см, а ширина \( BC \) равна 5 см. Чтобы найти площадь, нужно умножить эти две величины: \( AB \cdot BC = 6 \cdot 5 = 30 \, \text{см}^2 \). Это стандартная формула для площади прямоугольника, которая показывает, сколько квадратных сантиметров занимает фигура на плоскости.

Диагональ \( AC \) делит прямоугольник на два равных треугольника: \( \triangle ABC \) и \( \triangle ACD \). Это происходит потому, что диагональ соединяет две противоположные вершины, и каждая из этих частей занимает ровно половину площади всего прямоугольника. Таким образом, площадь каждого треугольника равна половине площади прямоугольника. Чтобы найти площадь одного треугольника, нужно площадь прямоугольника разделить на 2: \( \frac{30}{2} = 15 \, \text{см}^2 \).

Формула площади треугольника, если известны основания и высота, выглядит как \( \frac{1}{2} \times \text{основание} \times \text{высота} \). В нашем случае основание — это сторона \( AB \), а высота — сторона \( BC \), так как прямоугольник расположен так, что \( AB \) и \( BC \) перпендикулярны. Поэтому площадь треугольника \( ABC \) равна \( \frac{AB \cdot BC}{2} = \frac{6 \cdot 5}{2} = 15 \, \text{см}^2 \). Аналогично площадь треугольника \( ACD \) равна той же величине, поскольку оба треугольника равны по площади.

Ответ: площадь треугольников \( ABC \) и \( ACD \) равна по \( 15 \, \text{см}^2 \).