ГДЗ по Математике 5 Класс Часть 1 Номер 726 Мнемозина Виленкин, Жохов — Подробные Ответы

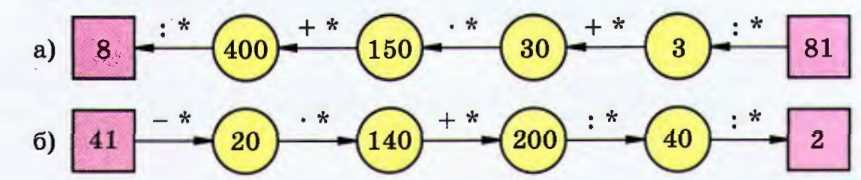
Восстановите цепочку вычислений, поставив вместо звёздочек пропущенные числа:

а)
Решаем уравнение \(81 : x = 3\), находим \(x = 81 : 3 = 27\).
Далее \(3 + y = 30\), значит \(y = 30 — 3 = 27\).
Из уравнения \(30 \cdot z = 150\) получаем \(z = 150 : 30 = 5\).
Для \(150 + a = 400\) вычисляем \(a = 400 — 150 = 250\).
Из \(400 : b = 8\) находим \(b = 400 : 8 = 50\).

Проверяем: \(81 : 27 = 3\), \(3 + 27 = 30\), \(30 \cdot 5 = 150\), \(150 + 250 = 400\), \(400 : 50 = 8\).

б)
Решаем \(41 — x = 20\), получаем \(x = 41 — 20 = 21\).
Из \(20 \cdot y = 140\) вычисляем \(y = 140 : 20 = 7\).
Для \(140 + z = 200\) находим \(z = 200 — 140 = 60\).
Из \(200 : a = 40\) получаем \(a = 200 : 40 = 5\).
Из \(40 : b = 2\) вычисляем \(b = 40 : 2 = 20\).

Проверяем: \(41 — 21 = 20\), \(20 \cdot 7 = 140\), \(140 + 60 = 200\), \(200 : 5 = 40\), \(40 : 20 = 2\).

а)
Для начала решаем уравнение \(81 : x = 3\). Здесь нужно найти число \(x\), при делении 81 на которое получится 3. Это значит, что \(x\) — это частное от деления 81 на 3, то есть \(x = 81 : 3 = 27\). Таким образом, мы нашли первое неизвестное значение.

Далее рассматриваем уравнение \(3 + y = 30\). Чтобы найти \(y\), нужно из 30 вычесть 3, так как \(y\) — это то, что прибавляется к 3, чтобы получить 30. Получаем \(y = 30 — 3 = 27\). Далее у нас есть уравнение \(30 \cdot z = 150\), где \(z\) — множитель, при умножении на 30 дающий 150. Чтобы найти \(z\), делим 150 на 30: \(z = 150 : 30 = 5\).

Теперь переходим к уравнению \(150 + a = 400\). Здесь \(a\) — число, которое нужно прибавить к 150, чтобы получить 400. Вычитаем 150 из 400: \(a = 400 — 150 = 250\). Следующее уравнение — \(400 : b = 8\), где \(b\) — делитель, при делении 400 на который получается 8. Значит, \(b = 400 : 8 = 50\).

Подставляя найденные значения, проверяем равенство: \(81 : 27 = 3\), \(3 + 27 = 30\), \(30 \cdot 5 = 150\), \(150 + 250 = 400\), \(400 : 50 = 8\). Все равенства верны, что подтверждает правильность решения.

б)
Рассмотрим уравнение \(41 — x = 20\). Чтобы найти \(x\), вычитаем 20 из 41, так как \(x\) — число, которое нужно вычесть из 41, чтобы получить 20. Получаем \(x = 41 — 20 = 21\). Следующее уравнение — \(20 \cdot y = 140\), где \(y\) — множитель, который при умножении на 20 дает 140. Чтобы найти \(y\), делим 140 на 20: \(y = 140 : 20 = 7\).

Далее уравнение \(140 + z = 200\) означает, что \(z\) — число, которое прибавляется к 140, чтобы получить 200. Вычитаем 140 из 200: \(z = 200 — 140 = 60\). Переходим к уравнению \(200 : a = 40\), где \(a\) — делитель, при делении 200 на который получается 40. Значит, \(a = 200 : 40 = 5\).

Последнее уравнение — \(40 : b = 2\), где \(b\) — число, на которое надо разделить 40, чтобы получить 2. Следовательно, \(b = 40 : 2 = 20\). Подставим все найденные значения: \(41 — 21 = 20\), \(20 \cdot 7 = 140\), \(140 + 60 = 200\), \(200 : 5 = 40\), \(40 : 20 = 2\). Все равенства выполняются, что подтверждает корректность решения.