ГДЗ по Математике 5 Класс Часть 1 Номер 626 Мнемозина Виленкин, Жохов — Подробные Ответы

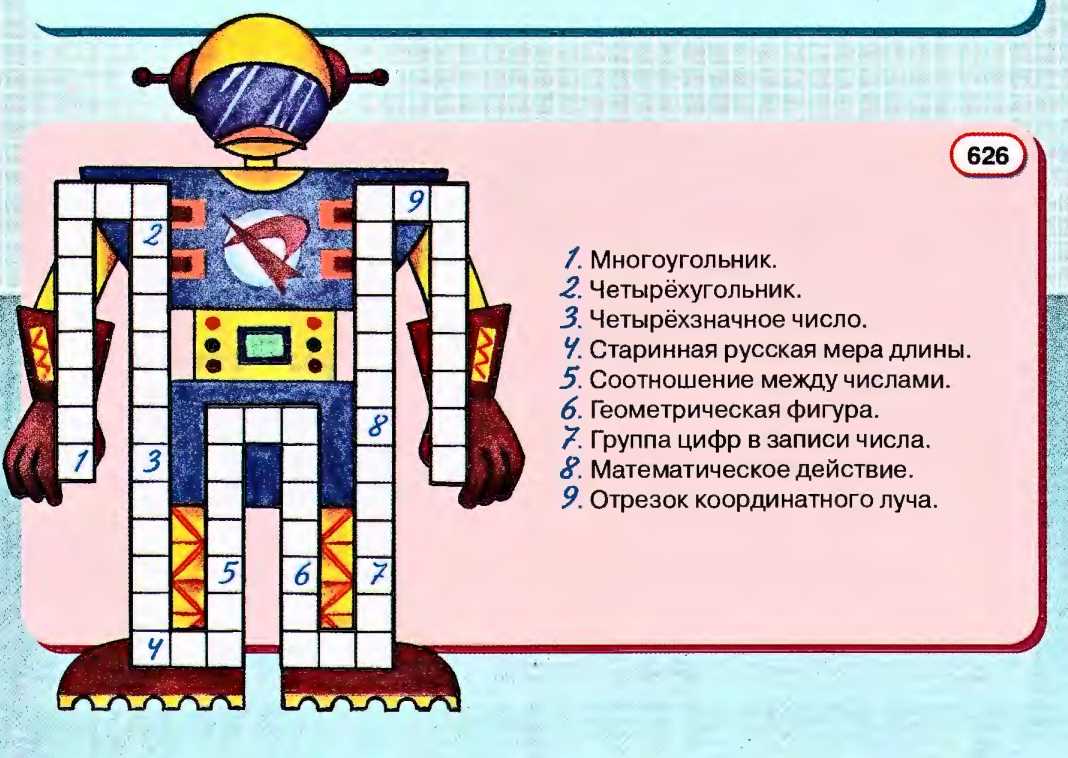
Разгадайте чайнворд, помещённый на форзаце в конце учебника.

1. Многоугольник — фигура с многими углами, например, треугольник.

2. Четырёхугольник — геометрическая фигура с четырьмя углами, например, квадрат.

3. Четырёхзначное число — число из четырёх цифр, например, тысяча.

4. Старинная русская мера длины — аршин.

5. Соотношение между числами — неравенство.

6. Геометрическая фигура — отрезок.

7. Группа цифр в записи числа — класс.

8. Математическое действие — сложение.

9. Отрезок координатного луча — единичный отрезок.

1. Многоугольник — это геометрическая фигура, которая состоит из нескольких отрезков, соединённых последовательно таким образом, что образуют замкнутую ломаную линию. Каждый такой отрезок называется стороной многоугольника, а точки их соединения — вершинами. Важно, что многоугольник имеет не менее трёх сторон, и все они лежат в одной плоскости. Например, треугольник — самый простой многоугольник, состоящий из трёх сторон и трёх углов.

Многоугольники бывают различных видов: выпуклые и невыпуклые, правильные и неправильные. Правильный многоугольник — это такой, у которого все стороны равны по длине, а все углы равны по величине. Для треугольника, например, равносторонний треугольник является правильным многоугольником. Многоугольники широко используются в математике и геометрии для изучения свойств фигур и вычисления различных величин, таких как площадь и периметр.

2. Четырёхугольник — это частный случай многоугольника, у которого ровно четыре стороны и четыре угла. Он может иметь различные формы: квадрат, прямоугольник, ромб, трапеция и другие. Квадрат — это правильный четырёхугольник, у которого все стороны равны и все углы прямые, то есть равны \(90^\circ\). Четырёхугольники играют важную роль в геометрии, так как многие реальные объекты имеют форму, близкую к четырёхугольникам.

Четырёхугольники изучаются с помощью различных теорем и свойств. Например, сумма всех внутренних углов четырёхугольника всегда равна \(360^\circ\). Это можно выразить формулой для многоугольника с \(n\) сторонами: сумма углов равна \((n-2) \times 180^\circ\), где при \(n=4\) получается \(2 \times 180^\circ = 360^\circ\). Понимание этих свойств помогает решать задачи на вычисление углов, сторон и площадей.

3. Четырёхзначное число — это число, состоящее из четырёх цифр, расположенных в определённом порядке. Например, число тысяча записывается как \(1000\), где цифра 1 стоит в позиции тысяч, а остальные три цифры — нули. Каждая цифра в числе имеет свой разряд: тысячи, сотни, десятки и единицы. Значение числа определяется суммой произведений каждой цифры на соответствующую степень десяти: \(a \times 10^3 + b \times 10^2 + c \times 10^1 + d \times 10^0\).

Четырёхзначные числа охватывают диапазон от \(1000\) до \(9999\). Они важны для понимания системы счисления и разрядных значений. В математике и повседневной жизни такие числа используются для обозначения больших количеств, например, населения, расстояний или денежных сумм. Понимание структуры числа помогает выполнять арифметические операции и анализировать числовые данные.

4. Аршин — это старинная русская мера длины, которая использовалась до введения метрической системы. Один аршин равнялся примерно \(0{,}7112\) метра. Эта мера длины применялась для измерения тканей, земельных участков и других объектов в быту и торговле. Аршин делился на части, например, вершки, что облегчало точные измерения.

Исторически аршин был важной единицей измерения, пока не был заменён метрической системой в XIX веке. Знание старинных мер длины помогает лучше понимать исторические документы и тексты, а также сравнивать старые и современные единицы измерения. В математике и физике важно уметь переводить значения из одной системы в другую для корректных расчётов.

5. Неравенство — это математическое выражение, которое показывает отношение между двумя величинами, когда они не равны, а одна больше или меньше другой. Например, \(a > b\) означает, что число \(a\) больше числа \(b\), а \(x \leq y\) означает, что \(x\) меньше или равно \(y\). Неравенства используются для описания диапазонов значений, ограничений и условий в задачах.

Неравенства играют ключевую роль в алгебре и анализе. Они позволяют решать задачи, где нужно найти множество значений переменной, удовлетворяющих определённым условиям. Например, решение неравенства \(2x + 3 > 7\) требует нахождения таких \(x\), для которых выполняется это условие. Неравенства также используются в экономике, физике и других науках для моделирования реальных ситуаций.

6. Отрезок — это часть прямой, ограниченная двумя точками, которые называются концами отрезка. Отрезок имеет определённую длину, которую можно измерить, в отличие от прямой, которая бесконечна. Отрезок обозначается двумя буквами, например, \(AB\), где \(A\) и \(B\) — его концы. Длина отрезка равна расстоянию между этими точками.

В геометрии отрезки служат основой для построения фигур и измерения расстояний. Например, стороны треугольника или квадрата — это отрезки. Отрезок можно разделить на части, найти его середину, провести через него перпендикуляры и использовать в различных построениях. Понимание свойств отрезка важно для решения задач на координатной плоскости и в пространстве.

7. Класс — это группа цифр в записи числа, которая помогает структурировать число по разрядам. В десятичной системе счисления число делится на классы по три цифры, начиная справа: единицы, тысячи, миллионы и так далее. Например, в числе \(1 234 567\) цифры \(567\) образуют класс единиц, \(234\) — класс тысяч, а \(1\) — класс миллионов.

Классы упрощают чтение и запись больших чисел, а также выполнение арифметических операций. Они позволяют легко определить порядок числа и его разрядность. В математике и экономике понимание классов чисел важно для работы с большими величинами и точного представления данных.

8. Сложение — это одно из основных арифметических действий, при котором две или более величины объединяются в одну сумму. Обозначается знаком \(+\). Например, \(3 + 5 = 8\). Сложение обладает свойствами коммутативности и ассоциативности, то есть порядок и группировка слагаемых не влияют на результат.

Сложение используется во всех сферах жизни и науки для подсчёта, объединения данных и решения задач. Оно является базовой операцией для дальнейших математических действий, таких как вычитание, умножение и деление. Понимание сложения важно для развития математического мышления и решения прикладных задач.

9. Единичный отрезок — это отрезок координатного луча, длина которого равна единице измерения. Он служит эталоном для измерения расстояний на числовой оси. Например, если на числовой оси отмечены точки \(0\) и \(1\), то отрезок между ними — единичный. Все остальные точки координатного луча измеряются относительно этого отрезка.

Единичный отрезок важен для построения координатных систем и измерения числовых величин. Он позволяет однозначно определить расстояния между точками и проводить вычисления с координатами. В аналитической геометрии и математическом анализе единичный отрезок является фундаментальной единицей для изучения функций и графиков.