
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 1 Номер 604 Мнемозина Виленкин, Жохов — Подробные Ответы
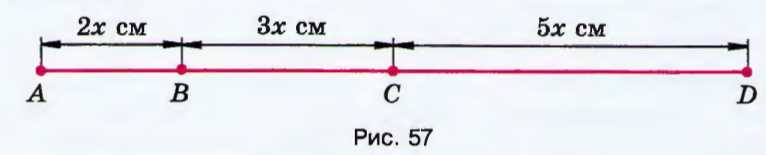
По рисунку 57 найдите длину отрезка \(BC\), если \(AD = 40\) см.
\(AB + BC + CD = AD\).
\(AB = 2x\) см; \(BC = 3x\) см; \(CD = 5x\) см; \(AD = 40\) см.
Составим уравнение:
\(2x + 3x + 5x = 40\)
\(10x = 40\)
\(x = \frac{40}{10}\)
\(x = 4\).
\(BC = 3x = 3 \cdot 4 = 12\) см.
Ответ: \(BC = 12\) см.
\(AB + BC + CD = AD\). Это уравнение отражает геометрическое свойство, где сумма длин трех отрезков равна длине четвертого. В условии даны выражения для каждого отрезка через переменную \(x\): \(AB = 2x\) см, \(BC = 3x\) см, \(CD = 5x\) см, а длина \(AD\) равна 40 см. Чтобы найти длину отрезка \(BC\), сначала нужно определить значение \(x\).
Для этого составим уравнение, подставив известные выражения в исходное равенство: \(2x + 3x + 5x = 40\). Сложив коэффициенты при \(x\), получаем \(10x = 40\). Это простое линейное уравнение, которое решается делением обеих частей на 10, что даёт \(x = \frac{40}{10}\). Таким образом, \(x = 4\).
Теперь, зная \(x\), можно найти длину отрезка \(BC\), подставив значение в выражение \(BC = 3x\). Получаем \(BC = 3 \cdot 4 = 12\) см. Это и есть искомая длина отрезка \(BC\). Ответ: \(BC = 12\) см.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!