ГДЗ по Математике 5 Класс Часть 1 Номер 602 Мнемозина Виленкин, Жохов — Подробные Ответы

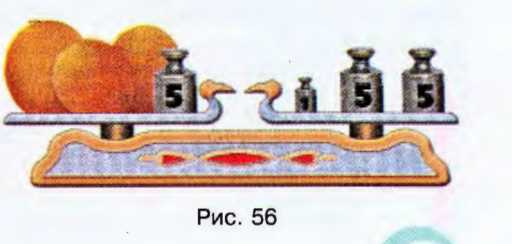
По рисунку 56 составьте уравнение и найдите массу каждой дыни. (Масса гирь дана в килограммах.)

Пусть масса каждой дыни равна \( x \) кг.

На левой чаше весов 3 дыни и гиря весом 5 кг,
на правой — три гири весом 1 кг, 5 кг и 5 кг.

Составим уравнение равновесия:
\( 3x + 5 = 1 + 5 \cdot 2 \)
\( 3x + 5 = 1 + 10 \)
\( 3x + 5 = 11 \)
\( 3x = 11 — 5 \)
\( 3x = 6 \)
\( x = \frac{6}{3} \)
\( x = 2 \) кг — масса каждой дыни.

Ответ: 2 кг.

Пусть масса каждой дыни равна \( x \) килограмм. Это предположение сделано для того, чтобы выразить общий вес нескольких одинаковых по массе предметов через одну переменную. В нашем случае, поскольку все дыни имеют одинаковый вес, вес трёх дынь будет равен \( 3x \) килограмм. Это позволяет перейти от конкретных чисел к алгебраическому выражению, что упрощает решение задачи.

На левой чаше весов находятся три дыни и гиря весом 5 килограмм. Вес левой чаши можно записать как сумму веса дынь и гири, то есть \( 3x + 5 \) килограмм. На правой чаше находятся три гири, вес которых равен 1 килограмму, 5 килограммам и ещё 5 килограммам. Сложив их, получаем общий вес правой чаши: \( 1 + 5 + 5 = 11 \) килограмм. Для удобства записи и понимания уравнения весов, правую часть можно представить как \( 1 + 5 \cdot 2 \), где \( 5 \cdot 2 \) — это сумма двух гирь по 5 килограмм.

Поскольку весы находятся в равновесии, веса на обеих чашах равны. Поэтому составляем уравнение: \( 3x + 5 = 1 + 5 \cdot 2 \). Раскроем скобки и упростим правую часть: \( 3x + 5 = 1 + 10 \), что даёт \( 3x + 5 = 11 \). Чтобы найти \( x \), сначала вычтем 5 из обеих частей уравнения: \( 3x = 11 — 5 \), то есть \( 3x = 6 \). Теперь разделим обе части на 3: \( x = \frac{6}{3} \). Получаем \( x = 2 \), что означает, что масса каждой дыни равна 2 килограммам.