ГДЗ по Математике 5 Класс Часть 1 Номер 572 Мнемозина Виленкин, Жохов — Подробные Ответы

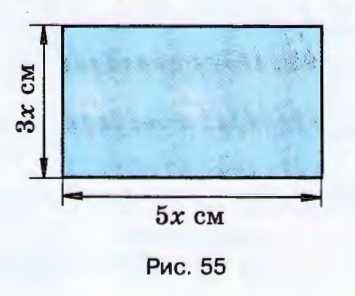
Чему равны стороны прямоугольника на рисунке 55, если его периметр равен 240 см?

Составим уравнение по условию: \( P = 2 \cdot (a + b) \).

\( 2 \cdot (3x + 5x) = 240 \)

\( 2 \cdot 8x = 240 \)

\( 8x = \frac{240}{2} \)

\( 8x = 120 \)

\( x = \frac{120}{8} = 15 \).

Тогда стороны прямоугольника:

\( 3x = 3 \cdot 15 = 45 \) см;

\( 5x = 5 \cdot 15 = 75 \) см.

Ответ: 45 см и 75 см.

а) В условии задачи дан периметр прямоугольника, который равен 240 см, и даны выражения для его сторон через переменную \(x\): одна сторона равна \(3x\), другая — \(5x\). Периметр прямоугольника вычисляется по формуле \(P = 2 \cdot (a + b)\), где \(a\) и \(b\) — длины сторон. Подставляем данные выражения: \(P = 2 \cdot (3x + 5x)\). Это значит, что сумма длин двух разных сторон умножается на 2, так как прямоугольник имеет две пары равных сторон.

Далее упрощаем выражение в скобках: \(3x + 5x = 8x\). Тогда уравнение для периметра принимает вид \(2 \cdot 8x = 240\). Это уравнение показывает, что удвоенная сумма сторон равна 240 см. Чтобы найти \(x\), сначала сократим уравнение, разделив обе части на 2, так как это упростит вычисления и позволит выразить переменную напрямую.

б) После сокращения уравнения получаем \(8x = \frac{240}{2}\), то есть \(8x = 120\). Это означает, что восемь частей длины стороны равны 120 см. Чтобы найти длину одной части \(x\), нужно разделить 120 на 8. Деление даёт точное значение, поскольку 8 умещается в 120 ровно 15 раз. Таким образом, \(x = \frac{120}{8} = 15\).

Значение \(x\) — ключ к нахождению реальных размеров сторон прямоугольника, так как стороны выражены через \(x\). Теперь можно подставить найденное число в выражения для сторон, чтобы получить конкретные размеры в сантиметрах.

в) Подставляя \(x = 15\) в выражение для первой стороны, получаем \(3x = 3 \cdot 15 = 45\) см. Это длина одной из сторон прямоугольника. Аналогично, для второй стороны: \(5x = 5 \cdot 15 = 75\) см. Эти значения показывают реальные размеры прямоугольника, которые удовлетворяют условию задачи и дают периметр 240 см при проверке.

Таким образом, стороны прямоугольника равны 45 см и 75 см, что подтверждается исходным уравнением и вычислениями. Эти размеры можно использовать для дальнейших расчетов, например, площади или других параметров фигуры.