ГДЗ по Математике 5 Класс Часть 1 Номер 550 Мнемозина Виленкин, Жохов — Подробные Ответы

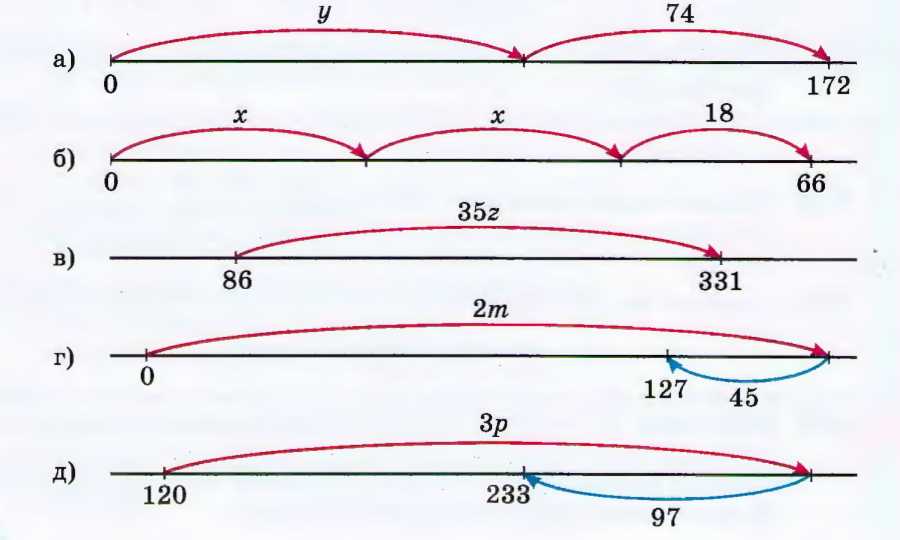
Используя рисунок, составьте и решите уравнение:

а) \(0 + y + 74 = 172\)
\(y + 74 = 172\)
\(y = 172 — 74\)
\(y = 98\)
Ответ: 98.

б) \(0 + x + x + 18 = 66\)
\(2x + 18 = 66\)
\(2x = 66 — 18\)
\(2x = 48\)
\(x = \frac{48}{2}\)
\(x = 24\)
Ответ: 24.

в) \(86 + 35z = 331\)
\(35z = 331 — 86\)
\(35z = 245\)
\(z = \frac{245}{35}\)
\(z = 7\)
Ответ: 7.

г) \(0 + 2m — 45 = 127\)
\(2m = 127 + 45\)
\(2m = 172\)
\(m = \frac{172}{2}\)
\(m = 86\)
Ответ: 86.

д) \(120 + 3p — 97 = 233\)
\(3p + (120 — 97) = 233\)
\(3p + 23 = 233\)
\(3p = 233 — 23\)
\(3p = 210\)
\(p = \frac{210}{3}\)
\(p = 70\)
Ответ: 70.

а) В уравнении \(0 + y + 74 = 172\) сначала убираем ноль, так как он не влияет на сумму, и получаем \(y + 74 = 172\). Это линейное уравнение с одной переменной \(y\), где нам нужно найти значение \(y\), при котором равенство выполняется. Чтобы найти \(y\), нужно из правой части уравнения вычесть 74, так как 74 — это число, которое прибавляется к \(y\).

Выполняем вычитание: \(y = 172 — 74\). Производя вычисление, получаем \(y = 98\). Это означает, что если к числу 98 прибавить 74, сумма будет равна 172, что подтверждает правильность решения. Таким образом, ответ: \(y = 98\).

б) Рассмотрим уравнение \(0 + x + x + 18 = 66\). Здесь ноль можно опустить, так как он не влияет на сумму. Осталось \(x + x + 18 = 66\), что можно переписать как \(2x + 18 = 66\), поскольку \(x + x = 2x\). Теперь нужно изолировать переменную \(x\), для этого сначала вычтем 18 из обеих частей уравнения.

Получим \(2x = 66 — 18\), что равно \(2x = 48\). Чтобы найти \(x\), делим обе части уравнения на 2: \(x = \frac{48}{2}\). Выполнив деление, получаем \(x = 24\). Это значение \(x\) удовлетворяет исходному уравнению, так как \(24 + 24 + 18 = 66\). Ответ: \(x = 24\).

в) В уравнении \(86 + 35z = 331\) нужно найти \(z\). Для этого сначала перенесём число 86 на правую сторону, изменив знак, чтобы оставить переменную \(z\) слева. Получаем \(35z = 331 — 86\). Вычисляем разность: \(35z = 245\).

Теперь, чтобы найти \(z\), делим обе части уравнения на 35: \(z = \frac{245}{35}\). Выполнив деление, получаем \(z = 7\). Это означает, что если умножить 7 на 35 и прибавить 86, получится 331. Ответ: \(z = 7\).

г) В уравнении \(0 + 2m — 45 = 127\) ноль можно опустить, остаётся \(2m — 45 = 127\). Чтобы найти \(m\), сначала прибавим 45 к обеим частям уравнения, чтобы избавиться от вычитания: \(2m = 127 + 45\).

Складываем правую часть: \(2m = 172\). Теперь делим обе части уравнения на 2, чтобы найти \(m\): \(m = \frac{172}{2}\). Выполнив деление, получаем \(m = 86\). Это значение удовлетворяет исходному уравнению. Ответ: \(m = 86\).

д) Уравнение \(120 + 3p — 97 = 233\) можно упростить, объединив числа \(120\) и \(-97\) слева: \(3p + (120 — 97) = 233\). Вычисляем разность: \(3p + 23 = 233\).

Далее вычитаем 23 из обеих частей уравнения, чтобы изолировать \(3p\): \(3p = 233 — 23\). Получаем \(3p = 210\). Для нахождения \(p\) делим обе части уравнения на 3: \(p = \frac{210}{3}\). Выполнив деление, получаем \(p = 70\). Ответ: \(p = 70\).