ГДЗ по Математике 5 Класс Часть 1 Номер 388 Мнемозина Виленкин, Жохов — Подробные Ответы

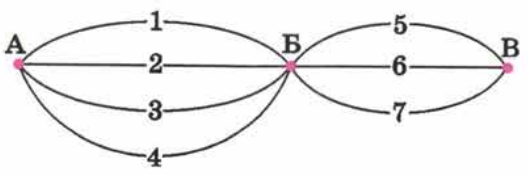
Из села Аникеево в село Большово ведут четыре дороги, а из села Большово в село Виноградово − три дороги. Сколькими способами можно добраться из Аникеева в Виноградово через село Большово?

Если из А в Б добираться по 1−й дороге, то продолжить путь есть три способа:

Точно так же рассуждая, получаем по три способа продолжить путь, начав добираться и по 2−й, и по 3−й, и по 4−й дороге. Значит, всего получается 4 * 3 = 12 способов добраться из Аникеева в Виноградово.

1. Рассмотрим задачу: нам необходимо найти количество способов добраться из точки А (Аникеево) в точку Б (Виноградово) через четыре возможные дороги, учитывая, что на каждой дороге можно продолжить путь тремя способами.

2. Начнем с первого этапа: из точки А в точку Б ведет несколько дорог. Пусть первая дорога является основной дорогой, по которой начнем движение. По этой дороге существует 3 варианта продолжения пути. Таким образом, если мы выбираем первую дорогу, то для каждого варианта продолжения будет еще три способа:

$$3 \text{ способа продолжить путь по 1-й дороге}.$$

3. Далее мы рассматриваем остальные три дороги. То есть, точно так же, если мы начнем движение по второй дороге, то для каждой из 3 возможных развилок будет также 3 способа продолжения пути. То же самое для третьей и четвертой дорог.

$$\text{Для 2-й дороги } 3 \text{ способа продолжить путь}.$$ $$\text{Для 3-й дороги } 3 \text{ способа продолжить путь}.$$ $$\text{Для 4-й дороги } 3 \text{ способа продолжить путь}.$$

4. Теперь нам нужно посчитать общее количество способов добраться из Аникеева в Виноградово. Поскольку существует 4 дороги, и для каждой из них есть 3 способа продолжить путь, нужно умножить количество возможных дорог (4) на количество вариантов для каждой дороги (3):

$$4 \times 3 = 12$$

5. Таким образом, общее количество способов добраться из Аникеева в Виноградово составляет 12.

Ответ:

$$\boxed{12 \text{ способов}}.$$