ГДЗ по Математике 5 Класс Часть 1 Номер 386 Мнемозина Виленкин, Жохов — Подробные Ответы

Найдите пропущенное число:

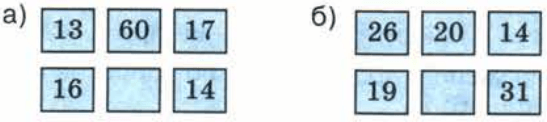
Решение а

Число: 60. Правило: среднее число равно удвоенной сумме крайних чисел.

Решение б

1. Решение a: Число 60. Правило: среднее число равно удвоенной сумме крайних чисел.

1.1. Разбор задачи:

Нам нужно найти среднее число, используя правило, что оно равно удвоенной сумме крайних чисел. Обозначим крайние числа как $a$ и $b$, а среднее число — как $m$.

Правило гласит:

$$m = 2(a + b)$$

Здесь $a$ и $b$ — крайние числа, а $m$ — среднее число. В данной задаче задано, что $m = 60$. Необходимо определить, какие значения могут принимать крайние числа $a$ и $b$, если их сумма удваивается, чтобы получить 60.

1.2. Подстановка значения среднего числа в уравнение:

Подставим $m = 60$ в формулу:

$$60 = 2(a + b)$$

1.3. Упростим уравнение:

Чтобы избавиться от коэффициента 2, разделим обе части уравнения на 2:

$$30 = a + b$$

Теперь мы знаем, что сумма крайних чисел равна 30:

$$a + b = 30$$

1.4. Разбор:

Сумма крайних чисел $a$ и $b$ должна быть равна 30, а их удвоенная сумма даст среднее число 60. Таким образом, любые два числа, сумма которых равна 30, удовлетворяют этому правилу. Например:

• Если $a = 10$, то $b = 20$.
• Если $a = 15$, то $b = 15$.
• Если $a = 25$, то $b = 5$.

1.5. Заключение:

Таким образом, ответ на задачу следующий:

$$a + b = 30$$

При этом среднее число $m = 60$ для всех таких чисел.

2. Решение б: Число 25. Правило: среднее число равно полусумме крайних чисел.

2.1. Разбор задачи:

В данном случае правило гласит, что среднее число $m$ равно полусумме крайних чисел $a$ и $b$. То есть:

$$m = \frac{a + b}{2}$$

Нам дано, что $m = 25$, и необходимо найти такие крайние числа $a$ и $b$, сумма которых, деленная на 2, равна 25.

2.2. Подстановка значения среднего числа в уравнение:

Подставим $m = 25$ в формулу:

$$25 = \frac{a + b}{2}$$

2.3. Упростим уравнение:

Чтобы избавиться от знаменателя 2, умножим обе части уравнения на 2:

$$50 = a + b$$

Теперь мы знаем, что сумма крайних чисел $a$ и $b$ должна быть равна 50:

$$a + b = 50$$

2.4. Разбор:

Сумма крайних чисел $a$ и $b$ должна быть равна 50, и среднее число $m = 25$ будет равно полусумме этих чисел. Как и в предыдущем решении, это означает, что любые два числа, сумма которых равна 50, будут удовлетворять этому правилу. Например:

• Если $a = 20$, то $b = 30$.
• Если $a = 25$, то $b = 25$.
• Если $a = 10$, то $b = 40$.

2.5. Заключение:

Таким образом, ответ на задачу следующий:

$$a + b = 50$$

При этом среднее число $m = 25$ для всех таких чисел.