
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 1 Номер 257 Мнемозина Виленкин, Жохов — Подробные Ответы
а) 4984 — 3561 = 1423
б) 23246 — 6728 = 16518
в) 15680 — 7397 = 8283
г) 38135 — 289 = 37846
а)
В выражении звёздочки обозначают неизвестные цифры.
Начнём с подбора чисел для того, чтобы разница между двумя числами давала 1423.
Проверяем выражение:
Это верно, так как:
Теперь, исходя из этого, мы видим, что:
Первая звёздочка в должна быть 9, чтобы получить число 4984.
Вторая звёздочка в должна быть 5, чтобы получить число 3561.
Ответ: 4984 — 3561 = 1423
б)
В выражении мы подставляем цифры и проверяем, какое вычитание дает число 16518.
Проверяем выражение:
Это верно, так как:
Анализируя это, мы получаем:
Первая звёздочка в должна быть 2, чтобы получилось число 23246.
Вторая звёздочка в должна быть 6, чтобы получилось число 6728.
Ответ: 23246 — 6728 = 16518
в)
В выражении подставляем цифры и проверяем вычитание.
Проверяем выражение:
Это верно, так как:
Исходя из этого:
Первая звёздочка в должна быть 1, чтобы получилось число 15680.
Вторая звёздочка в должна быть 8, чтобы получилось число 8283.
Ответ: 15680 — 7397 = 8283
г)
В выражении подставляем цифры и проверяем вычитание.
Проверяем выражение:
Это верно, так как:
Таким образом:
Первая звёздочка в должна быть 3, чтобы получилось число 38135.
Вторая звёздочка в должна быть 9, чтобы получилось число 289.
Третья звёздочка в должна быть 4, чтобы получилось число 37846.
Ответ: 38135 — 289 = 37846
Итоговые ответы:
а)
б)
в)
г)
Заключение:
Задача сводится к подстановке цифр, чтобы проверка выражений с вычитанием дала корректные результаты. В каждом случае мы нашли правильные цифры, заменив звёздочки, и подтверждали результаты, вычисляя разность.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


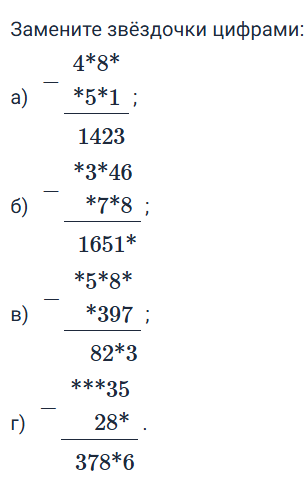



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!