ГДЗ по Математике 5 Класс Часть 2 Номер 6.235 Виленкин, Жохов — Подробные Ответы

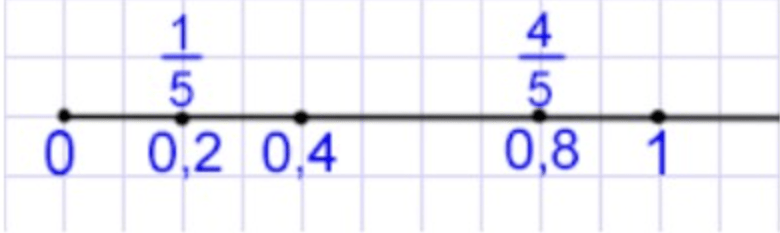
а) Объясните, как на координатном луче отметить числа  , 0,2, 0,4 и 0,8.
б) Найдите равные дроби.
в) Какой дроби со знаменателем 5 равна дробь 0,6?
г) Найдите суммы  + 0,25 двумя способами, обратив обыкновенные дроби в десятичные и десятичные в обыкновенные.

а) Нужно выбрать единичный отрезок в 10 клеток.

• $10 : 5 = 2$ (клетки) — составляет дробь $\frac{1}{5}$;
• $10 : 5 \cdot 4 = 8$ (клеток) — составляет дробь $\frac{4}{5}$;
• 2 клетки — составляет дробь $0,2$;
• 4 клетки — составляет дробь $0,4$;
• 8 клеток — составляет дробь $0,8$.

б) $0,2 = \frac{1}{5}$ и $0,8 = \frac{4}{5}$.

в) $0,6 = \frac{6}{10} = \frac{3}{5}$

г)

$$\frac{4}{5} + 0,2 = \frac{8}{10} + 0,2 = 0,8 + 0,2 = 1$$ $$\frac{4}{5} + 0,2 = \frac{4}{5} + \frac{2}{10} = \frac{4}{5} + \frac{1}{5} = \frac{5}{5} = 1$$ $$\frac{1}{5} + 0,25 = \frac{2}{10} + 0,25 = 0,2 + 0,25 = 0,45$$ $$\frac{1}{5} + 0,25 = \frac{1}{5} + \frac{25}{100} = \frac{1}{5} + \frac{5}{20} = \frac{4}{20} + \frac{5}{20} = \frac{9}{20} = \frac{45}{100}$$

а) Объяснение того, как на координатном луче отметить числа $0.2$, $0.4$ и $0.8$.

Единичный отрезок: В задаче сказано, что единичный отрезок делится на 10 равных частей (клеток). Это означает, что каждый отрезок равен $\frac{1}{10}$ единицы.

Отметка числа $0.2$: Число $0.2$ — это 2 десятых, то есть $\frac{2}{10}$. Чтобы отметить это число на координатном луче:

Разделите отрезок от 0 до 1 на 10 равных частей.

Отметьте вторую клетку. Это и будет $0.2$.

Отметка числа $0.4$: Число $0.4$ — это 4 десятых, то есть $\frac{4}{10}$. Чтобы отметить это число:

Отметьте 4-ю клетку на отрезке. Это и будет $0.4$.

Отметка числа $0.8$: Число $0.8$ — это 8 десятых, то есть $\frac{8}{10}$. Чтобы отметить это число:

Отметьте 8-ю клетку. Это и будет $0.8$.

Таким образом, на координатном луче числа $0.2$, $0.4$ и $0.8$ будут расположены в зависимости от их десятичной записи и соответствующих клеток.

б) Найдите равные дроби.

Для числа $0.2$:

• $0.2=\frac{2}{10}$.
• Уменьшаем дробь $\frac{2}{10}$, деля числитель и знаменатель на 2:

$$\frac{2}{10}=\frac{1}{5}\mathrm{.}$$

Таким образом, $0.2=\frac{1}{5}$.

Для числа $0.8$:

• $0.8=\frac{8}{10}$.
• Уменьшаем дробь $\frac{8}{10}$, деля числитель и знаменатель на 2:

$$\frac{8}{10}=\frac{4}{5}\mathrm{.}$$

Таким образом, $0.8=\frac{4}{5}$.

Ответ: $0.2=\frac{1}{5},0.8=\frac{4}{5}$.

в) Какой дроби со знаменателем 5 равна дробь $0.6$?

Запишем число $0.6$ как дробь:

$$0.6=\frac{6}{10}\mathrm{.}$$

Чтобы привести эту дробь к знаменателю 5, умножим числитель и знаменатель на 2:

$$\frac{6}{10}=\frac{6\times 2}{10\times 2}=\frac{12}{20}\mathrm{.}$$

Умножаем числитель и знаменатель на 2, чтобы получить дробь со знаменателем 5:

$$\frac{6}{10}=\frac{3}{5}\mathrm{.}$$

Ответ: $0.6=\frac{3}{5}$.

г) Найдите суммы двумя способами:

Обе дроби в десятичной форме, потом сумма, или же перевести десятичные в обыкновенные и выполнить сложение.

Первый способ — используя десятичные числа:

$\frac{4}{5}+0.2=0.8+0.2=1$.

Здесь $\frac{4}{5}$ записано как $0.8$, а $0.2$ остается как есть. Складываем $0.8$ и $0.2$, получаем $1$.

$\frac{4}{5}+0.2=\frac{4}{5}+\frac{2}{10}=\frac{4}{5}+\frac{1}{5}=\frac{5}{5}=1$.

Сначала приводим $0.2$ к дроби $\frac{2}{10}$, а затем складываем дроби с одинаковым знаменателем. Получаем $\frac{5}{5}=1$.

Второй способ — используя обыкновенные дроби:

$\frac{1}{5}+0.25=\frac{2}{10}+0.25=0.2+0.25=0.45$.

Число $0.25$ преобразуем в дробь $\frac{1}{4}$, а затем складываем обе дроби.

$\frac{1}{5}+0.25=\frac{1}{5}+\frac{25}{100}=\frac{1}{5}+\frac{5}{20}=\frac{4}{20}+\frac{5}{20}=\frac{9}{20}=\frac{45}{100}$.

Преобразуем дробь в десятичное число, приводя к общей дроби.

Ответ:

$$\frac{4}{5}+0.2=1\text{и}\frac{1}{5}+0.25=0.45\text{или}\frac{45}{100}\mathrm{.}$$

Ответ:

$$\boxed{{\displaystyle \text{а) }\frac{1}{5},\frac{4}{5},0.2,0.4,0.8;\text{б) }0.2=\frac{1}{5},0.8=\frac{4}{5};\text{в) }0.6=\frac{3}{5};\text{г) }1,0.45,\frac{45}{100}}}$$