
ГДЗ по математике 5 класс к учебнику Виленкина, Жохова – это незаменимый помощник для школьников, осваивающих основы математики. Он помогает лучше понять материал, закрепить навыки и успешно справляться с домашними заданиями.
ГДЗ по Математике 5 Класс Часть 2 Номер 5.420 Виленкин, Жохов — Подробные Ответы
Найдите разность a/14 − 1/a при а = 7; а = 8; а = 4.
Общее решение:
Для каждого значения нужно привести дроби к общему знаменателю и выполнить вычитание. Приведем подробное решение для каждого случая.
При :
- Подставляем значение в исходное выражение:
- Приводим дроби к общему знаменателю. Общий знаменатель для и равен 14. Приводим дробь к знаменателю 14:
- Теперь вычитаем дроби с одинаковыми знаменателями:
При :
- Подставляем значение в исходное выражение:
- Приводим дроби к общему знаменателю. Общий знаменатель для и равен 56. Приводим дроби к знаменателю 56:
- Теперь вычитаем дроби с одинаковыми знаменателями:
При :
- Подставляем значение в исходное выражение:
- Приводим дроби к общему знаменателю. Общий знаменатель для и равен 28. Приводим дроби к знаменателю 28:
- Теперь вычитаем дроби с одинаковыми знаменателями:
Заключение:
Ответы для каждого значения следующие:
- При , результат равен
- При , результат равен
- При , результат равен

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


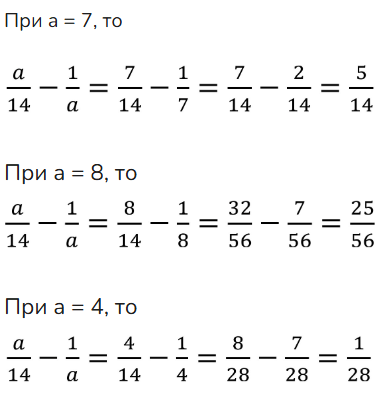



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!