ГДЗ по Математике 5 Класс Часть 2 Номер 5.222 Виленкин, Жохов — Подробные Ответы

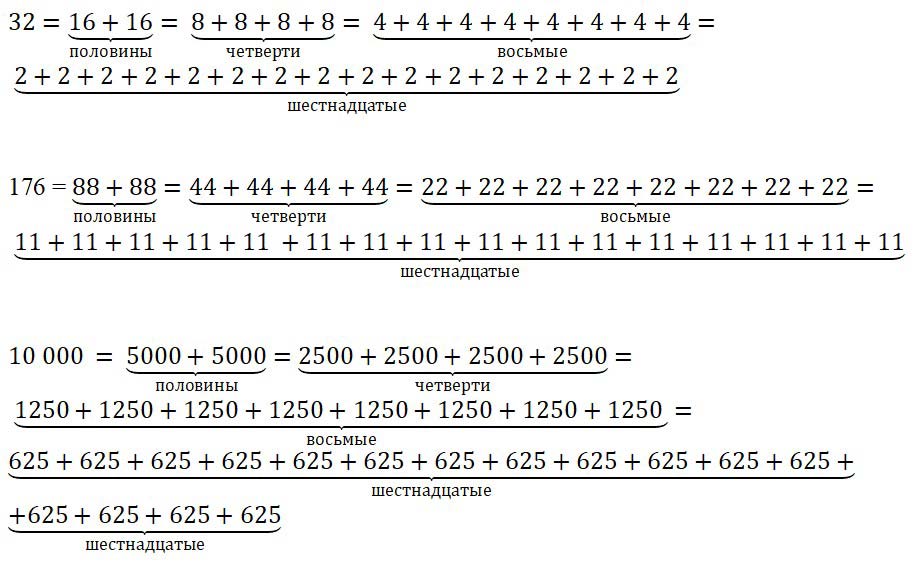
Числа 32, 176, 10 000 представьте в виде суммы их половин, четвертей, восьмых, шестнадцатых.

Пример 1: 32

Шаг 1:
Записываем 32 как сумму двух одинаковых чисел:

$$32=16+16$$

Это выражение соответствует делению 32 пополам. Мы разделили 32 на 2 части по 16.

Шаг 2:
Делим 16 на более мелкие части:

$$32=8+8+8+8$$

Здесь мы разделили каждое из 16 на 2 части, то есть на 8. В результате мы получаем 4 части по 8.

Шаг 3:
Продолжаем разбиение на еще более мелкие части:

$$32=4+4+4+4+4+4+4+4$$

Здесь каждое из 8 было разделено еще пополам, что дает 8 частей по 4.

Шаг 4:
Теперь переходим к частям более мелкого размера:

$$32=2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2$$

Каждое из 4 теперь делим пополам, получая 16 частей по 2.

Шаг 5:
Это можно представить как половины, четверти, восьмые, и шестнадцатые (так как мы делим на все более мелкие части).

Пример 2: 176

Шаг 1:
Записываем 176 как сумму двух одинаковых чисел:

$$176=88+88$$

Мы разделили 176 пополам.

Шаг 2:
Делим 88 на более мелкие части:

$$176=44+44+44+44$$

Теперь разделили 88 на 4 части по 44.

Шаг 3:
Делим 44 на еще более мелкие части:

$$176=22+22+22+22+22+22+22+22$$

Здесь каждое из 44 делим пополам, что дает 8 частей по 22.

Шаг 4:
Делим 22 на более мелкие части:

$$176=11+11+11+11+11+11+11+11+11+$$

$$11+11+11+11+11+11+11$$

Каждое из 22 делим пополам, получая 16 частей по 11.

Шаг 5:
Это можно также представить как половины, четверти, восьмые, и шестнадцатые.

Пример 3: 10 000

Шаг 1:
Записываем 10 000 как сумму двух одинаковых чисел:

$$10000=5000+5000$$

Здесь мы разделили 10 000 пополам.

Шаг 2:
Делим 5000 на более мелкие части:

$$10000=2500+2500+2500+2500$$

Теперь 5000 делим на 4 части по 2500.

Шаг 3:
Делим 2500 на еще более мелкие части:

$$10000=1250+1250+1250+1250+1250+1250+1250+1250$$

Теперь каждое из 2500 делим пополам, получая 8 частей по 1250.

Шаг 4:
Делим 1250 на еще более мелкие части:

$$10000=625+625+625+625+625+625+625+625+625+625+$$

$$625+625+625+625+625+625$$

Каждое из 1250 делим пополам, получая 16 частей по 625.

Шаг 5:
Это представление снова можно назвать половинами, четвертями, восьмыми и шестнадцатыми.